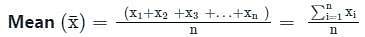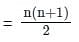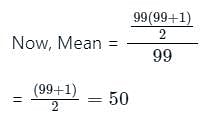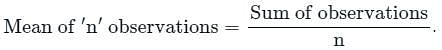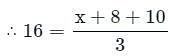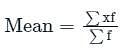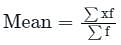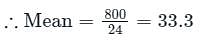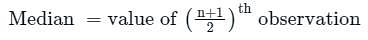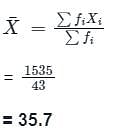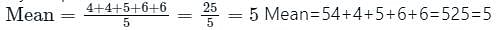MCQ: Measures of Central Tendency and Variation - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Measures of Central Tendency and Variation
What is the mean of first 99 natural numbers?
Let the average of three numbers be 16. If two of the numbers are 8 and 10, what is the remaining number?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
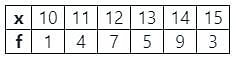
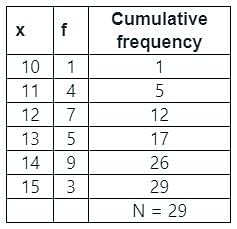
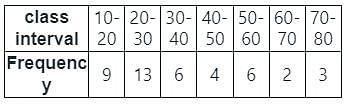
Find the mode and the median of the following frequency distribution respectively.
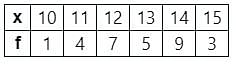

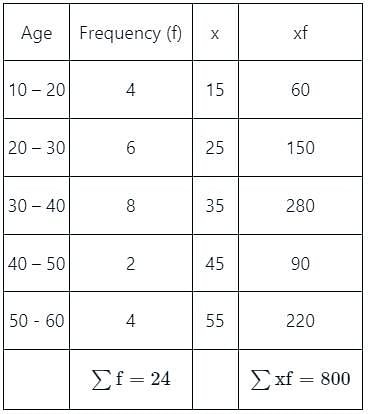
A random sample of 24 people is classified in the following table according to their ages:

What is the mean age of this group of people?
Find the no. of observations between 250 and 300 from the following data:

If the mode of the following data is 7, then the value of k in the data set 3, 8, 6, 7, 1, 6, 10, 6, 7, 2k + 5, 9, 7, and 13 is:
Find the median of the given set of numbers 2, 6, 6, 8, 4, 2, 7, 9
If mean and mode of some data are 4 & 10 respectively, its median will be:
What is the mean of the range, mode and median of the data given below?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
The mean of 20 numbers is zero. Of them, at the most, how many may be greater than zero?
Which of the following is the correct formula for the arithmetic mean?
The number of observations smaller than _________ is the same as the number of observations larger than it.
For the given set of data: 4, 4, 5, 6, 6 which of the following is true?
The mean monthly salary paid to 77 employees in a company was Rs. 78. The mean salary of 32 of them was Rs. 45 and of the other 25 was Rs. 82. What was the mean salary of the remaining?