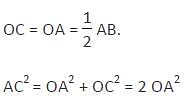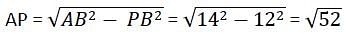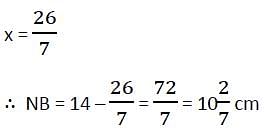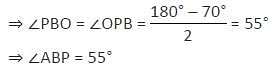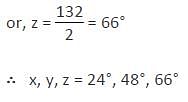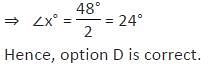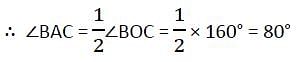MCQ: Circles - 3 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Circles - 3
Directions: Kindly study the following question carefully and choose the right answer:
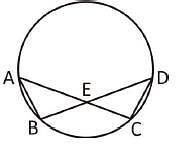
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°, ∠BAC is
Directions: Kindly study the following question carefully and choose the right answer:
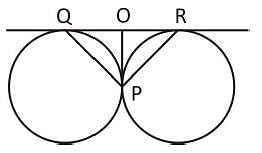
Two circles touch externally at P, QR is a common tangent of the circles touching the circles at Q and R. Then measure of ∠QPR is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
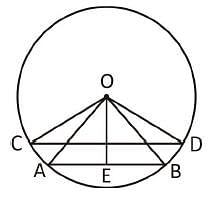
Directions: Kindly study the following question carefully and choose the right answer:
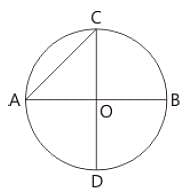
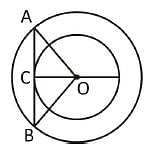
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is :
Directions: Kindly study the following question carefully and choose the right answer:
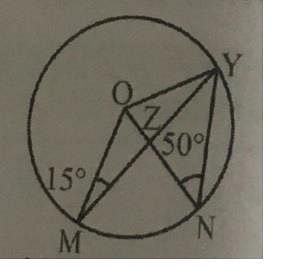
In the given figure, ∠ONY = 50° and ∠OMY = 15°. Then the value of the ∠MON is
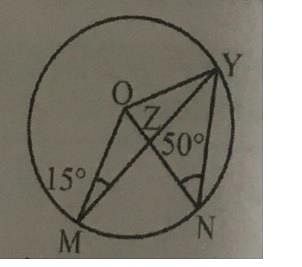
Directions: Kindly study the following question carefully and choose the right answer:
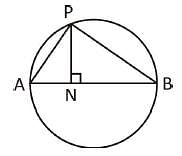
N is the foot of the perpendicular from a point P of a circle with radius 7 cm, on a diameter AB of the circle. If the length of the chord PB is 12 cm, the distance of the point N from the point B is
Directions: Kindly study the following question carefully and choose the right answer:
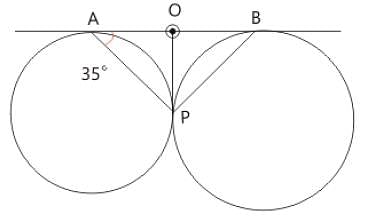
Two circles touch each other externally at P. AB is a direct common tangent to the two circles, A and B are points of contact and ∠PAB = 35° . Then ∠ABP is is
Directions: Kindly study the following question carefully and choose the right answer:
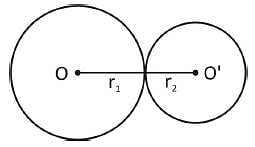
Two circles touch each other externally. The distance between their centre is 7 cm. If the radius of one circle is 4 cm, then the radius of the other circle is
Directions: Kindly study the following question carefully and choose the right answer:
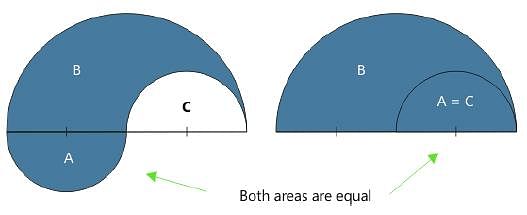
What is the area (in cm2) of shaded portion bounded by three semicircle as shown in the figure? (It is given that the radius of two smaller semicircle is 1 cm)
Directions: Kindly study the following question carefully and choose the right answer:
If two concentric circles are of radii 5 cm and 3 cm, then the length of the chord of the larger circle which touches the smaller circle is
Directions: Kindly study the following question carefully and choose the right answer:
A, B, C are three points on the circumference of a circle and if AB = AC = 5 √2 cm and ∠BAC = 90°, find the radius.
Directions: Kindly study the following question carefully and choose the right answer:
In ΔABC, ∠ABC = 70°, ∠BCA = 40°. O is the point of intersection of the perpendicular bisectors of the sides, and then the angle ∠BOC is
Directions: Kindly study the following question carefully and choose the right answer:
In the given figure ‘O’ is the centre of the circle and PAT is the tangent at point A. Find the measures of x°, y°, and z° respectively.
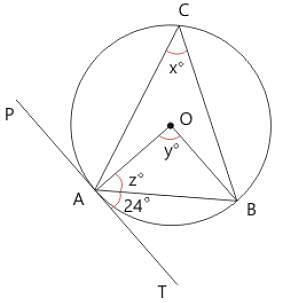
Directions: Kindly study the following question carefully and choose the right answer:
Two chords of lengths a metre and b metre subtend angles 60° and 90° at the centre of the circle respectively. Which of the following is true ?
Directions: Kindly study the following question carefully and choose the right answer:
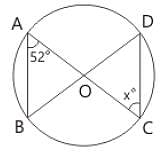
O is the centre of the circle. if ∠BAC = 52°, then ∠OCD is equal to
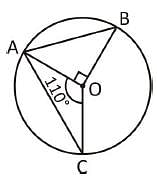
Directions: Kindly study the following question carefully and choose the right answer:
A, B and C are the three points on a circle such that the angles subtended by the chords AB and AC at the centre O are 90° and 110° respectively. ∠BAC is equal to