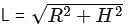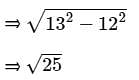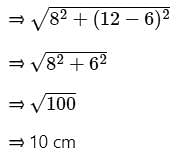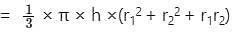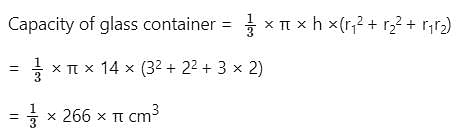MCQ: Cone - 2 - SSC CGL MCQ
10 Questions MCQ Test - MCQ: Cone - 2
The slant height of a right circular cone is 13 cm, and the area of the base is 144π cm². Find the volume (in cm³) of the cone.
Height and radius of a cone are 15 cm and 7 cm, respectively. What is the volume of the cone?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The circumference of the base of a 16 cm height solid cone is 33 cm. What is the volume of the cone in cm3?
The curved surface area of a right circular cone of radius 28 cm is 4664 cm². What is the slant height of the cone? (Use π=22/7)
The slant height and radius of a cone are 30 cm and 14 cm, respectively. What is the total surface area of the cone?
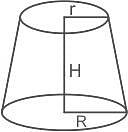
The height of the frustum of a cone is 8 cm. The radius on the top of the frustum is 6 cm and the bottom of the frustum is 12 cm. What is the curved surface area of the frustum?
The circumference of base of cone is 132 cm. The difference between the slant height and radius of base is 8 cm. Find the volume of cone.
The height and the slant height of a right circular cone are given as 3√23 cm and 16 cm respectively. Approximating π by 22/7, find the curved surface area of the same cone.
A glass container is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 6 cm and 4 cm. Find the capacity of the container.
The frustum of a right circular cone has the radius of the base as 5 cm, radius of the top as 3 cm, and height as 6 cm. What is its volume?