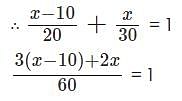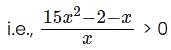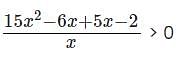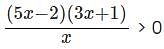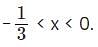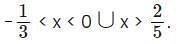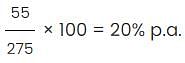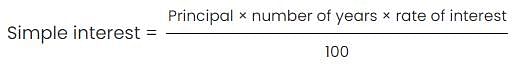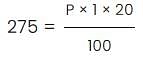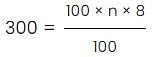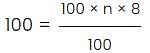GMAT Focus Edition Mock test - 1 - GMAT MCQ
30 Questions MCQ Test - GMAT Focus Edition Mock test - 1
Peter invested a certain sum of money in a simple interest bond whose value grew to $300 at the end of 3 years and to $ 400 at the end of another 5 years. What was the rate of interest in which he invested his sum?
In a class 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the curve described by the equation y = x2 + bx + c cuts the x-axis at -4 and y axis at 4, at which other point does it cut the x-axis?
An analysis of the monthly incentives received by 5 salesmen : The mean and median of the incentives is $7000. The only mode among the observations is $12,000. Incentives paid to each salesman were in full thousands. What is the difference between the highest and the lowest incentive received by the 5 salesmen in the month?
What is the remainder when 1044 × 1047 × 1050 × 1053 is divided by 33?
Set A contains all the even numbers between 2 and 50 inclusive. Set B contains all the even numbers between 102 and 150 inclusive. What is the difference between the sum of elements of set B and that of set A?
Ram, who is half as efficient as Krish, will take 24 days to complete a task if he worked alone. If Ram and Krish worked together, how long will they take to complete the task?
What is the smallest integer that satisfies the inequality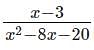 > 0?
> 0?
Ann invested a certain sum of money in a bank that paid simple interest. The amount grew to $240 at the end of 2 years. She waited for another 3 years and got a final amount of $300. What was the principal amount that she invested at the beginning?
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?
How many trailing zeros will be there after the rightmost non-zero digit in the value of 25!?
A can complete a project in 20 days and B can complete the same project in 30 days. If A and B start working on the project together and A quits 10 days before the project is completed, in how many days will the project be completed?
What range of values of 'x' will satisfy the inequality 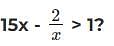
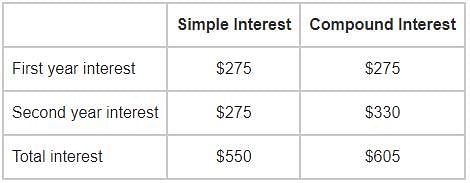
Shawn invested one half of his savings in a bond that paid simple interest for 2 years and received $ 550 as interest. He invested the remaining in a bond that paid compound interest, interest being compounded annually, for the same 2 years at the same rate of interest and received $605 as interest. What was the value of his total savings before investing in these two bonds?
How many keystrokes are needed to type numbers from 1 to 1000?
If "x" is an integer, which of the following inequalities has (have) a finite range of values of "x" satisfying it (them)?
Braun invested a certain sum of money at 8% p.a. simple interest for 'n' years. At the end of 'n' years, Braun got back 4 times his original investment. What is the value of n?
How many integral divisors does the number 120 have?
When 242 is divided by a certain divisor the remainder obtained is 8. When 698 is divided by the same divisor the remainder obtained is 9. However, when the sum of the two numbers 242 and 698 is divided by the divisor, the remainder obtained is 4. What is the value of the divisor?
A merchant who marked his goods up by 50% subsequently offered a discount of 20% on the marked price. What is the percentage profit that the merchant make after offering the discount?
A number when divided by a divisor leaves a remainder of 24. When twice the original number is divided by the same divisor, the remainder is 11. What is the value of the divisor?
In the twentieth century, the visual arts have embarked on major experimentation, from cubism to expressionism. While tastes always vary, there are certainly some people who find beautiful objects of each of the art movements of the first half of the twentieth century. In the latter half of the twentieth century, though, most works are so abstract or shocking that neither the critic nor the general public uses the word "beautiful" to describe them: indeed, sometimes late twentieth-century artists have, as one of their expressed goals, the creation of a work that no one could find beautiful. Whatever these artists are creating may be intellectually engaging at some level, but it is no longer art.
Q. Which of the following is an assumption that supports drawing the conclusion above from the reasons given for that conclusion?
In a few recent cases, some teenagers with advanced programming abilities used a new programming language, FANTOD, to hack into ETS and change their own SAT scores. All of the teenagers convicted of this crime were highly skilled in programming FANTOD. In light of these cases, some colleges have discounted the official SAT scores of applicants with a knowledge of FANTOD, and have required them to take special admission tests in supervised conditions on their own campuses.
Q. Which of following conclusions can most properly be drawn from the information above?
A minor league baseball franchise experienced a drop in attendance this week after they suffered three losses by margins of ten runs or more last week. Many spectators of those games wrote letters to the editors of the local sporting news, complaining of the poor play of the team in those three losses. Nevertheless, the front office of this baseball franchise maintains that the team's poor play in those three losses has nothing to do with this week's decline in attendance.
Q. Which of the following, if true, most strongly supports the position held by the front office of the baseball franchise?
Megalimpet is a nationwide owner of office space. They have major office buildings in the downtowns of several cities in the 48 lower states, and rent this space to individual companies. Megalimpet office spaces vary from small office to large suites, and every space has custom-designed wall-to-wall carpeting. The carpet in several Megalimpet facilities needed replacing. The winning bid for the nationwide carpet replacement was submitted by Bathyderm Carpet Company (BCC). The bid contract involves all delivery costs, all installation, and any ongoing maintenance and upkeep while the carpet is under the three-year warranty. Both BCC executives and independent consultants they hired felt BCC would be able to perform all these services for far less than their bid price; these circumstances would allow BCC to reap a considerable profit.
Q. Which of the following, if true, most calls in question the argument that BCC will make a large profit from this contract with Megalimpet?
Direction: Read the following Passage and Answer the following Question.
“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.
Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.
This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”
Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.
Q. Which of the following would be the most appropriate title for the passage?
Direction: Read the following Passage and Answer the following Question.
“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.
Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.
This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”
Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.
Q. It can be inferred from the passage that Harriet Sherman would be most likely to agree with which of the following statements regarding admission to museum exhibits?
Direction: Read the following Passage and Answer the following Question.
“Strange Bedfellows!” lamented the title of a recent letter to Museum News, in which a certain Harriet Sherman excoriated the National Gallery of Art in Washington for its handling of tickets to the much-ballyhooed “Van Gogh’s van Goghs” exhibit. A huge proportion of the 200,000 free tickets were snatched up by the opportunists in the dead of winter, who then scalped those tickets at $85 apiece to less hardy connoiseurs.
Yet, Sherman’s bedfellows are far from strange. Art, despite its religious and magical origins, very soon became a commercial venture. From bourgeois patrons funding art they barely understood in order to share their protegee’s prestige, to museum curators stage-managing the cult of artists in order to enhance the market value of museum holdings, entrepreneurs have found validation and profit in big-name art. Speculators, thieves, and promoters long ago created and fed a market where cultural icons could be traded like commodities.
This trend toward commodification of high-brow art took an ominous, if predictable, turn in the 1980s during the Japanese “bubble economy.” At a time when Japanese share prices more than doubled, individual tycoons and industrial giants alike invested record amounts in some of the West’s greatest masterpieces. Ryoei Saito, for example, purchased van Gogh’s Portrait of Dr. Gachet for a record-breaking $82.5 million. The work, then on loan to the Metropolitan Museum of Modern Art, suddenly vanished from the public domain. Later learning that he owed the Japanese government $24 million in taxes, Saito remarked that he would have the paining cremated with him to spare his heirs the inheritance tax. This statement, which he later dismissed as a joke, alarmed and enraged many. A representative of the Van Gogh museum, conceding that he had no legal redress, made an ethical appeal to Mr. Saito, asserting, “a work of art remains the possession of the world at large.”
Ethical appeals notwithstanding, great art will increasingly devolve into big business. Firstly, great art can only be certified by its market value. Moreover, the “world at large” hasn’t the means of acquisition. Only one museum currently has the funding to contend for the best pieces–the J. Paul Getty Museum, founded by the billionaire oilman. The art may disappear into private hands, but its transfer will disseminate once static fortunes into the hands of various investors, collectors, and occasionally the artist.
Q. The passage supplies information for answering which of the following questions?
A prominent investor who holds a large stake in the Burton Tool Company has recently claimed that the company is mismanaged, citing as evidence the company's failure to slow down production in response to a recent rise in its inventory of finished products. It is doubtful whether an investor's sniping at management can ever be anything other than counterproductive, but in this case, it is clearly not justified. It is true that an increased inventory of finished products often indicates that production is outstripping demand, but in Burton's case it indicates no such thing. Rather, the increase in inventory is entirely attributable to products that have already been assigned to orders received from customers.
Q. In the argument given, the two boldfaced portions play which of the following roles? (underline)
A child learning to play the piano will not succeed unless the child has an instrument at home on which to practice. However, good-quality pianos, whether new or secondhand, are costly. Buying one is justified only if the child has the necessary talent and perseverance, which is precisely what one cannot know in advance. Consequently, parents should buy an inexpensive secondhand instrument at first and upgrade if and when the child's ability and inclination are proven.
Q. Which of the following, if true, casts the most serious doubt on the course of action recommended for parents?


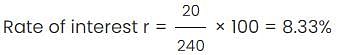
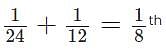 of the task in a day.
of the task in a day.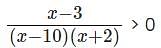
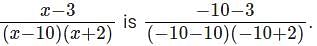
 the inequality holds good in this interval.
the inequality holds good in this interval.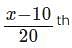 of the project in (x - 10) days.
of the project in (x - 10) days.