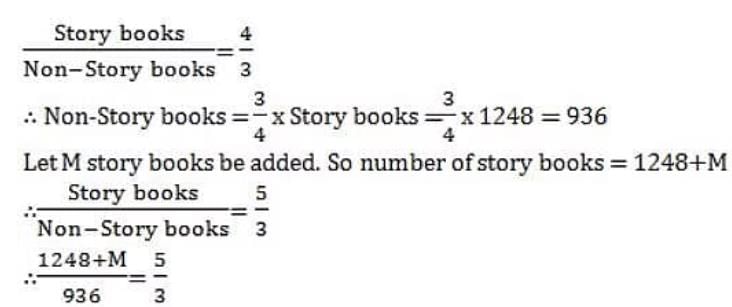Test: Ratio & Proportion (February 5) - CAT MCQ
10 Questions MCQ Test - Test: Ratio & Proportion (February 5)
If the work done by p men in (p + 2) days is to the work done by (p + 4) men in (p – 1) days is in the ratio 1 : 1, then the value of p is:
If A is 25% less than B, then what will be the value of (2B - A)/A ?
The monthly incomes of X and Y are in the ratio of 4:3 and their monthly expenses are in the ratio of 3:2. However, each saves Rs. 6,000 per month. What is their total monthly income?
The incomes of Sheldon, Leonard, and Howard are in the ratio of 4 : 5 : 6 respectively and their spending are in the ratio of 6 : 7 : 8 respectively. If Sheldon saves one fourth his income, then the savings of Sheldon, Leonard, and Howard are in the ratio:
A sum of Rs. 12,384 is divided between A, B, C and D such that the ratio of the shares of A and B is 3 : 4, that of B and C is 5 : 6, and that of C and D is 8 : 9. What is the share of C ?
In a library, the ratio of number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.
There are three persons A, B and C in a room. If a person D joins the room, the average weight of the persons in the room reduces by x kg. Instead of D, if person E joins the room, the average weight of the persons in the room increases by 2x kg. If the weight of E is 12 kg more than that of D, then the value of x is
A bag has ₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins. The coins are in the ratio of 6 : 9 : 10. How many coins of ₹ 5 are in the bag?
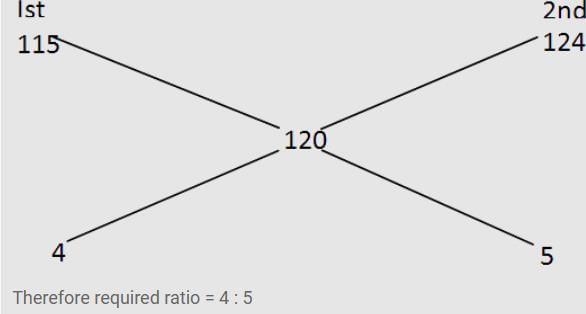
In what ratio must two kinds of sugar at Rs. 1.15 and Rs. 1.24 per kg be mixed so that by selling at Rs. 1.50 per kg, 25% may be gained
The sum of three numbers x, y, z is 5000. If we reduce the first number by 50, the second number by 100, and the third number by 150, then the new ratio of x & y = 4 : 5 & the new ratio of y & z =3 : 4. What is the value of x + y ?