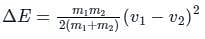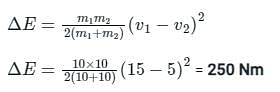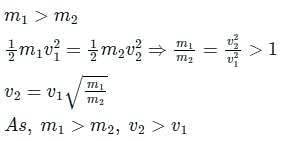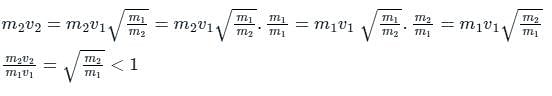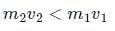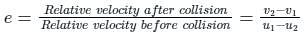Test: Impulse and Momentum- 2 - EmSAT Achieve MCQ
10 Questions MCQ Test - Test: Impulse and Momentum- 2
Two balls of equal mass and of Perfectly elastic material are lying on the floor. One of the balls with velocity V is made to struck with the second ball. Both the balls after impact will move with a velocity
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
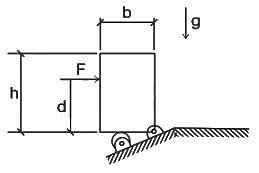
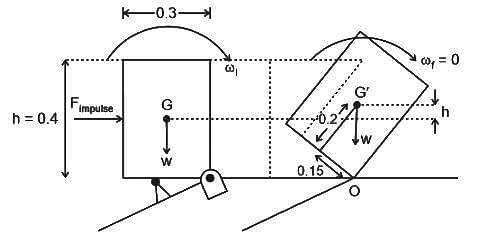
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s2), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse IF is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of IF required to topple the block is

The rate of change of momentum is equal to the applied force and it takes place in the direction of the force is a statement of:
Two inelastic spheres of masses 10 kg each move with velocities of 15 m/s and 5 m/s respectively in the same direction. The loss in kinetic energy when they collide
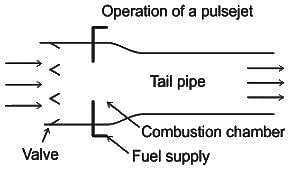
On which of the fundamental principle a jet engine works?
If light and a heavy body have an equal kinetic energy of translation, then ________.
During elastic and inelastic collision, ________ is conserved.
Calculate the velocity of a body having a mass of 9 kg and linear momentum of 63 kg m/s.



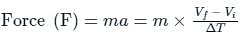
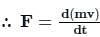
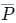 = change in momentum in that direction.
= change in momentum in that direction.