Mathematics Mock Test - 6 - CDS MCQ
30 Questions MCQ Test - Mathematics Mock Test - 6
Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result, the product went up by 540. What is the new product?
In a four-digit number, the sum of the first 2 digits is equal to that of the last 2 digits. The sum of the first and last digits is equal to the third digit. Finally, the sum of the second and fourth digits is twice the sum of the other 2 digits. What is the third digit of the number?
Rohan purchased some pens, pencils and erasers for his young brothers and sisters for the ensuing examinations. He had to buy atleast 11 pieces of each item in a manner that the number of pens purchased is more than the number of pencils, which is more than the number of erasers. He purchased a total of 38 pieces. If the number of pencils cannot be equally divided among his 4 brothers and sisters, how many pens did he purchase?
Seema has joined a new Company after the completion of her B.Tech from a reputed engineering college in Chennai. She saves 10% of her income in each of the first three months of her service and for every subsequent month, her savings are Rs. 50 more than the savings of the immediate previous month. If her joining income was Rs. 3000, her total savings from the start of the service will be Rs. 11400 in:
In a group of people, 28% of the members are young while the rest are old. If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
There are 7 members in a family whose average age is 25 years. Ram who is 12 years old is the second youngest in the family. Find the average age of the family in years just before Ram was born?
The average marks of a group of 20 students on a test is reduced by 4 when the topper who scored 90 marks is replaced by a new student. How many marks did the new student have?
If the work done by p men in (p + 2) days is to the work done by (p + 4) men in (p – 1) days is in the ratio 1 : 1, then the value of p is:
A person going from Pondicherry to Ootacamond travels 120 km by steamer, 450 km by rail and 60 km by horse transit. The journey occupies 13 hours 30 minutes, and the speed of the train is three times that of the horse-transit and 1(1/2) times that of the steamer. Find the speed of the train.
X can do a piece of work in 20 days. He worked at it for 5 days and then Y finished it in 15 days. In how many days can X and Y together finish the work?
Find the roots of the quadratic equation: x2 + 2x - 15 = 0?
If the roots of the equation 2x2 - 5x + b = 0 are in the ratio of 2:3, then find the value of b?
The number of solutions of the equation 2x + y = 40 where both x and y are positive integers and x <= y is:
A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.
3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10, and 12 seconds respectively. In 30 minutes, how many times do they toll together?
The product of two numbers is 4107. If the H.C.F. of these numbers is 37, then the greater number is:
By selling a cap for Rs. 29.75, a man gains 6.25%. What will be the CP of the cap?
A man sells a TV set for Rs. 33000 and makes a profit of 10%. He sells another TV at a loss of 20%. If on the whole, he neither gains nor loses, find the selling price of the second TV set.
Q. How much time will it take for an amount of Rs. 900 to yield Rs. 81 as interest at 4.5% per annum of simple interest?
Suresh for 2 years invested Rs. 500 in SBI. He also invested Rs. 300 in ICICI for 4 years. At the end he received Rs. 220 from both banks as simple interest. What must have been rate of interest? (assuming the rate of interest for both banks is same)
A die is rolled twice. What is the probability of getting a sum equal to 9?
John draws a card from a pack of cards. What is the probability that the card drawn is a card of black suit?
A train passes a platform in 36 seconds. The same train passes a man standing on the platform in 20 seconds. If the speed of the train is 54 km/hr, The length of the platform is:
Find the value of a/b + b/a, if a and b are the roots of the quadratic equation x2 + 8x + 4 = 0?
I. a2 - 9a + 20 = 0,
II. 2b2 - 5b - 12 = 0 to solve both the equations to find the values of a and b?



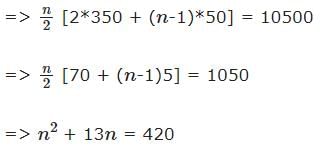
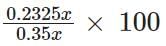
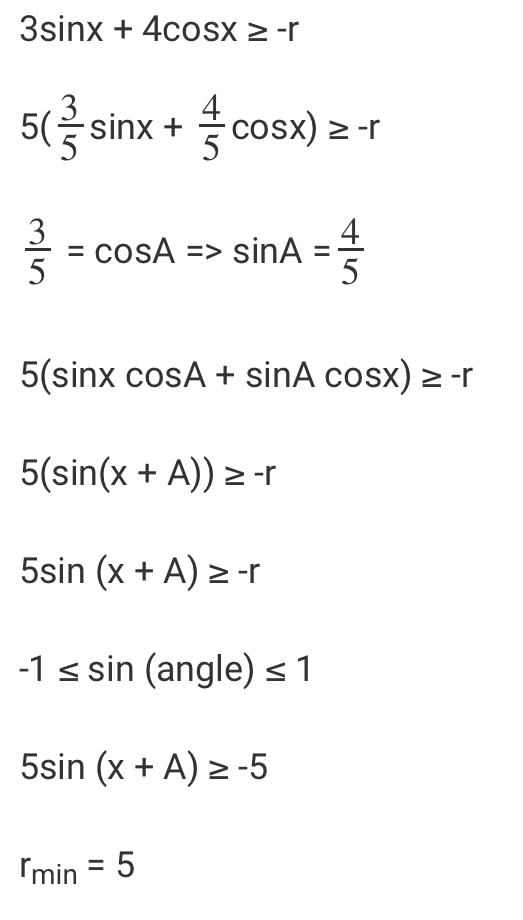
 ab = 3.
ab = 3. Greater number = 111.
Greater number = 111.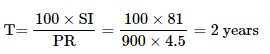
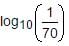 is equal to :
is equal to :