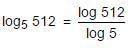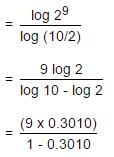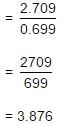Mathematics Mock Test - 7 - CDS MCQ
30 Questions MCQ Test - Mathematics Mock Test - 7
A red light flashes three times per minute and a green light flashes five times in 2 min at regular intervals. If both lights start flashing at the same time, how many times do they flash together in each hour?
All the page numbers from a book are added, beginning at page 1.
However, one page number was added twice by mistake. The sum obtained was 1000. Which page number was added twice?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A nursery has 363, 429 and 693 plants respectively of 3 distinct varieties. It is desired to place these plants in straight rows of plants of 1 variety only so that the number of rows required is the minimum. What is the size of each row and how many rows would be required?
Sailesh is working as a sales executive with a reputed FMCG Company in Hyderabad. As per the Company’s policy, Sailesh gets a commission of 6% on all sales upto Rs. 1,00,000 and 5% on all sales in excess of this amount. If Sailesh remits Rs. 2,65,000 to the FMCG company after deducting his commission, his total sales were worth:
Anil buys 12 toys and labels each with the same selling price. He sells 8 toys initially at 20% discount on the labeled price. Then he sells the remaining 4 toys at an additional 25% discount on the discounted price. Thus, he gets a total of Rs 2112, and makes a 10% profit. With no discounts, his percentage of profit would have been
The average weight of a class of 10 students is increased by 2 kg when one student of 30kg left and another student joined. After a few months, this new student left and another student joined whose weight was 10 less than the student who left now. What is the difference between the final and initial averages?
The incomes of Sheldon, Leonard, and Howard are in the ratio of 4 : 5 : 6 respectively and their spending are in the ratio of 6 : 7 : 8 respectively. If Sheldon saves one fourth his income, then the savings of Sheldon, Leonard, and Howard are in the ratio:
In a stream, Q lies in between P and R such that it is equidistant from both P and R. A boat can go from P to Q and back in 6 hours 30 minutes while it goes from P to R in 9 hours. How long would it take to go from R to P?
A dog sees a cat. It estimates that the cat is 25 leaps away. The cat sees the dog and starts running with the dog in hot pursuit. If in every minute, the dog makes 5 leaps and the cat makes 6 leaps and one leap of the dog is equal to 2 leaps of the cat. Find the time in which the cat is caught by the dog (assume an open field with no trees).
If the roots of the equation (a2 + b2)x2 − 2b(a + c)x + (b2+c2) = 0 are equal then
The sum of the squares of two consecutive positive integers exceeds their product by 91. Find the integers?
For a real number x the condition |3x - 20| + |3x - 40| = 20 necessarily holds if
Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
If sin (A + B) = √3 / 2 and tan (A – B) = 1. What are the values of A and B?
A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?
Three number are in the ratio of 3 : 4 : 5 and their L.C.M. is 2400. Their H.C.F. is:
Q. Find the greatest number that will divide 43, 91 and 183 so as to leave the same remainder in each case.
A machine costs Rs. 1025. If it is sold at a loss of 25%, what will be its cost price as a percentage of its selling price?
E sold at table to R at a profit of 25%.R sold the same table to S for Rs. 90 thereby making a profit of 20%. Find the price at which E bought the table from Z if it is known that Z gained 25% in the transaction.
Arun took a loan of Rs. 1400 with simple interest for as many years as the rate of interest. If he paid Rs.686 as interest at the end of the loan period, what was the rate of interest?
What will be the ratio of simple interest earned by certain amount at the same rate of interest for 5 years and that for 15 years?
Hunar wrote two sections of CAT paper; Verbal and QA in the same order. The probability of her passing both sections is 0.6. The probability of her passing the verbal section is 0.8. What is the probability of her passing the QA section given that she has passed the Verbal section?
Three coins are tossed. What is the probability of getting at most two tails?
If log 2 = 0.3010 and log 3 = 0.4771, the value of log5 512 is:
A train moves past a post and a platform 264 m long in 8 seconds and 20 seconds respectively. What is the speed of the train?
I. a2 + 11a + 30 = 0,
II. b2 + 6b + 5 = 0 to solve both the equations to find the values of a and b?