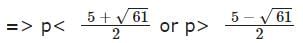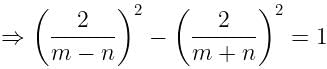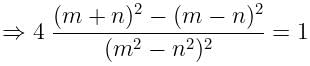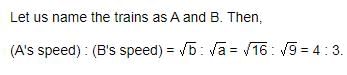Mathematics Mock Test - 9 - CDS MCQ
30 Questions MCQ Test - Mathematics Mock Test - 9
In some code, letters a, b, c, d and e represent numbers 2, 4, 5, 6 and 10. We just do not know which letter represents which number. Consider the following relationships:
I. a + c = e,
II. b – d = d and
III. e + a = b
Which of the following options are true?
II. b – d = d and
III. e + a = b
What is the least number of soldiers that can be drawn up in troops of 12, 15, 18 and 20 soldiers and also in form of a solid square?
1 ’s are given 100 times, 2 ’s are given 100 times and 3’s are given 100 times. Now numbers are made by arranging these 300 digits in all possible ways. How many of these numbers will be perfect squares?
The ratio of number of male and female journalists in a newspaper office is 5:4. The newspaper has two sections, political and sports. If 30 percent of the male journalists and 40 percent of the female journalists are covering political news, what percentage of the journalists (approx.) in the newspaper is currently involved in sports reporting?
The income of Amala is 20% more than that of Bimala and 20% less than that of Kamala. If Kamala’s income goes down by 4% and Bimala’s goes up by 10%, then the percentage by which Kamala’s income would exceed Bimala’s is nearest to
The average number of runs scored by Virat Kohli in four innings is 48. In the fifth inning, Kohli scores some runs such that his average now becomes 60. In the 6th innings he scores 12 runs more than his fifth innings and now the average of his last five innings becomes 78. How many runs did he score in his first innings? (He does not remain not out in any of the innings)
The mean temperature of Monday to Wednesday was 35 °C and of Tuesday to Thursday was 30 °C. If the temperature on Thursday was 1/2 that of Monday, the temperature on Thursday was ______ .
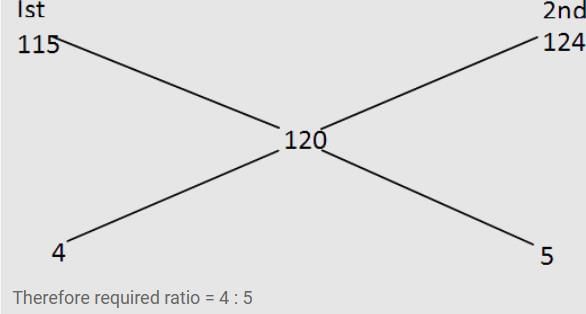
In what ratio must two kinds of sugar at Rs. 1.15 and Rs. 1.24 per kg be mixed so that by selling at Rs. 1.50 per kg, 25% may be gained
Sheldon had to cover a distance of 60 km. However, he started 6 minutes later than his scheduled time and raced at a speed 1 km/h higher than his originally planned speed and reached the finish at the time he would reach it if he began to race strictly at the appointed time and raced with the assumed speed. Find the speed at which he travelled during the journey described.
Charlie and Alan run a race between points A and B, 5 km apart. Charlie starts at 9 a.m. from A at a speed of 5 km/hr, reaches B, and returns to A at the same speed. Alan starts at 9:45 a.m. from A at a speed of 10 km/hr, reaches B and comes back to A at the same speed. At what time do Charlie and Alan first meet each other?
If the roots of a quadratic equation are 20 and -7, then find the equation?
The sum of the square of the three consecutive even natural numbers is 1460. Find the numbers?
The inequality of p2 + 5 < 5p + 14 can be satisfied if:
The minimum possible value of the sum of the squares of the roots of the equation x2 + (a + 3) x - (a + 5) = 0 is
If tanØ + sinØ = m, tanØ - sinØ = n, find the value of m2 - n2.
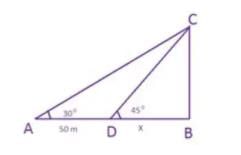
Anil looked up at the top of a lighthouse from his boat and found the angle of elevation to be 30 degrees. After sailing in a straight line 50 m towards the lighthouse, he found that the angle of elevation changed to 45 degrees. Find the height of the lighthouse.
The product of two numbers is 2028 and their H.C.F. is 13. The number of such pairs is:
Let N be the greatest number that will divide 1305, 4665 and 6905, leaving the same remainder in each case. Then sum of the digits in N is:
E owns a house worth Rs. 20,000. He sells it to R at a profit of 25%. After some time, R sells it back to E at 25% loss. Find E’s loss or gain per cent.
E sells a car priced at Rs. 1,80,000. He gives a discount of 5% on the first Rs. 1,00,000 and 12.5% on the remaining Rs. 80,000. His competitor R sells a car on the same market priced at Rs. 1,80,000. If he wants to be competitive what percent discount should R offer on the marked price.
A sum fetched a total simple interest of Rs. 929.20 at the rate of 8 p.c.p.a. in 5 years. What is the sum?
A certain amount earns simple interest of Rs. 1750 after 7 years. Had the interest been 2% more, how much more interest would it have earned?
One card is randomly drawn from a pack of 52 cards. What is the probability that the card drawn is a face card(Jack, Queen or King)
A bag contains 2 yellow, 3 green and 2 blue balls. Two balls are drawn at random. What is the probability that none of the balls drawn is blue?
If log10 5 + log10 (5x + 1) = log10 (x + 5) + 1, then x is equal to:
Two trains, one from P to Q and the other from Q to P, start simultaneously. After they meet, the trains reach their destinations after 9 hours and 16 hours respectively. The ratio of their speeds is
A man could buy a certain number of notebooks for Rs.300. If each notebook cost is Rs.5 more, he could have bought 10 notebooks less for the same amount. Find the price of each notebook?
I. a2 - 2a - 8 = 0,
II. b2 = 9 to solve both the equations to find the values of a and b?