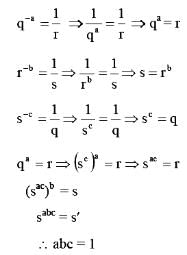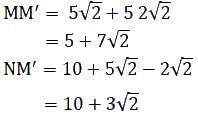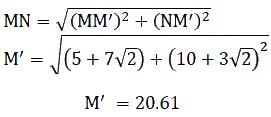General Aptitude - 5 - GATE Chemistry MCQ
20 Questions MCQ Test - General Aptitude - 5
40% of deaths on city roads may be attributed to drunken driving. The number of degree needed to represent this as a slice of a pie chart is
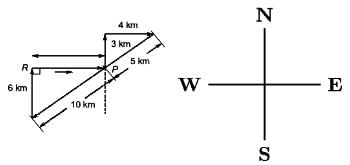
Fatima starts from point P, goes North for 3 km, and then East for 4km to reach point Q. She then turns to face point P and goes 15km in that direction. She then goes North for 6km. How far is she from point P, and in which direction should she go to reach point P?
The number of 3-digit numbers such that the digit 1 is never to the immediate right of 2 is
A person moving through a tuberculosis prone zone has a 50% probability of becoming infected.However, only 30% of infected people develop the disease. What percentage of people moving through a tuberculosis prone zone remains infected but does not show symptoms of disease?
P, Q, R and S are working on a project. Q can finish the task in 25 days, working alone for 12hours a day. R can finish the task in 50 days, working alone for 12 hours per day. Q worked 12 hours a day but took sick leave in the beginning for two days. R worked 18 hours a day on all days. What is the ratio of work done by Q and R after 7 days from the start of the project?
A rule states that in order to drink beer one must be over 18 years old. In a bar, there are 4 people. P is 16 years old, Q is 25 years old, R is drinking milkshake and S is drinking beer. What must be checked to ensure that the rule is being followed ?
500 students are taking one or more courses out of Chemistry, Physics, and Mathematics. Registration records indicate course enrolment as follows: Chemistry (329). Physics (186).Mathematics (295). Chemistry and Physics (83), Chemistry and Mathematics (217), and Physics and Mathematics (63). How many students are taking all 3 subjects?
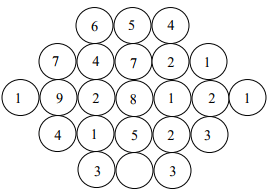
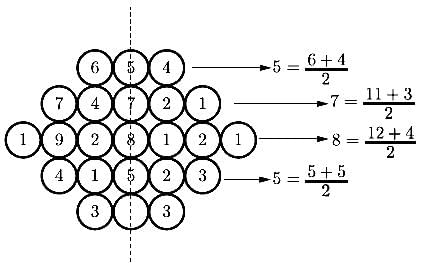
A contour line joins locations having the same height above the mean sea level. The following is a contour plot of a geographical region. Contour lines are shown at 25m intervals in this plot.
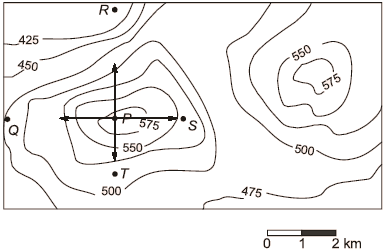
Q. Which of the following is the steepest path leaving from P?
Given (9 inches)1/2 = (0.25 yards) 1/2, which one of the following statements is TRUE?
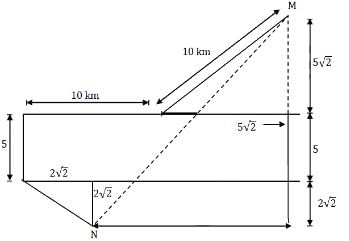
M and N start from the same location. M travels 10 km East and then 10 km North-East. N travels 5 km South and then 4 km South-East. What is the shortest distance (in km) between M and N at the end of their travel?
The number that least fits this set: (324, 441, 97 and 64) is _____.
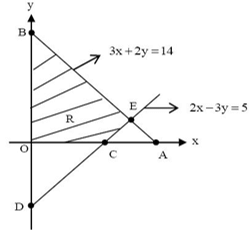
Find the area bounded by the lines 3x + 2y = 14, 2x - 3y = 5 in the first quadrant.
A straight line is fit to a data set (ln x, y). This line intercepts the abscissa at ln x = 0.1 and has a slope of −0.02. What is the value of y at x = 5 from the fit?
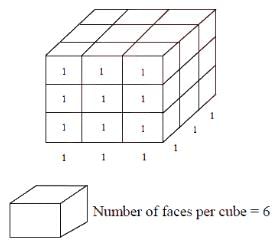
A cube of side 3 units is formed using a set of smaller cubes of side 1 unit. Find the proportion of the number of faces of the smaller cubes visible to those which are NOT visible.
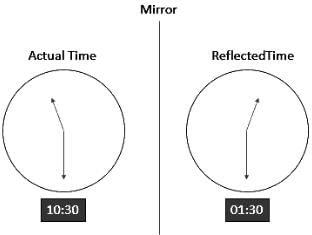
Two and a quarter hours back, when seen in a mirror, the reflection of a wall clock without number markings seemed to show 1:30. What is the actual current time shown by the clock?
A wire of length 340 mm is to be cut into two parts. One of the parts is to be made into a square and the other into a rectangle where sides are in the ratio of 1:2. What is the length of the side of the square (in mm) such that the combined area of the square and the rectangle is a MINIMUM?
It takes 10s and 15s, respectively, for two trains travelling at different constant speeds to completely pass a telegraph post. The length of the first train is 120 m and that of the second train is 150 m. The magnitude of the difference in the speeds of the two trains (in m/s) is _____.



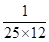
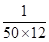
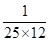
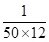
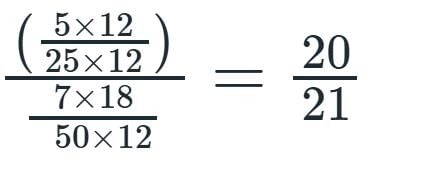
 , the value of abc is _____
, the value of abc is _____