Liquid Solution MCQ - 2 (Advanced) - JEE MCQ
20 Questions MCQ Test - Liquid Solution MCQ - 2 (Advanced)
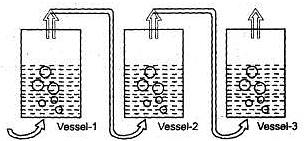
Dry air is slowly passed through three solutions of different concentrations, c,, c2 and c3 ; each containing (non volatile) NaCI as solute and water as solvent, as shown in the Fig. If the vessel 2 gains weight and the vessel 3 loses weight, then
In which of the following pairs of solutions will the values of the vent Hoff factor be the same?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Vapour pressure of solution containing 6g of a non-volatile solute in 180 g water is 20.0 Torr. If 1 mole water is further added vapour pressure increases by 0.02 Torr. Which of the following is true ?
Two liquids Aand B form an ideal solution. The solution has a vapor pressure of 700 Torr at 80°C. It is distilled till 2/3°' of the solution is collected as condensate. The composition of the condensate is x'A= 0.75 and that of the residue is x"A= 0.30. If the vapor pressure of the residue at 80°C is 600 Tom, which of the following is/ are true?
For chloroform and acetone or for a solution of chloroform and acetone if p, (observed (actual)) is compared with ps ( Theoretical ( Raoult) ) then which of the following is /are true ?
Consider two liquids ‘B’ and ‘C’ that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of ‘B’ and ‘C’ .We shall plot the system’s pressure P and against XB’ the overall mole fraction of B in the system :
Where nbl and nbv are the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBl and nBv may vary.
Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlb where xlb at D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoult's law, Pb=xvbPob relates the vapour-phase mole fractions to the liquid composition as follows:
Where Pob and Pocare the vapour pressures of pure 'B' and pure 'C' at T, where the system's pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.
Let B be the more volatile component, meaning that Pob>Poc Above equation then shows that Xvb/Xvc>Xlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D.
Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.
Q.
If the above process is repeated for all other compositions of mixture of C and B. If all the points where vapours start converting into liquid are connected and all the points where vapours get completely converted into liquid are connected then obtained graph will look like.
Consider two liquids ‘B’ and ‘C’ that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of ‘B’ and ‘C’ .We shall plot the system’s pressure P and against XB’ the overall mole fraction of B in the system :
Where nbl and nbv are the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBl and nBv may vary.
Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlb where xlb at D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoult's law, Pb=xvbPob relates the vapour-phase mole fractions to the liquid composition as follows:
Where Pob and Pocare the vapour pressures of pure 'B' and pure 'C' at T, where the system's pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.
Let B be the more volatile component, meaning that Pob>Poc Above equation then shows that Xvb/Xvc>Xlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D.
Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.
Q.
The equation of the curve obtained by connecting all those points where the vapors of above mixture (all mixtures of different composition are taken) just start forming will be
Consider two liquids ‘B’ and ‘C’ that form an ideal solutlion. We hold the temperature fixed at some value T that is above the freezing points of ‘B’ and ‘C’ .We shall plot the system’s pressure P and against XB’ the overall mole fraction of B in the system :
Where nbl and nbv are the number of moles of B in the liquid and vapor phases, respectively. For a close system xB, is fixed, although nBl and nBv may vary.
Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant-temperature bath.To see what the P-versus-xB phase diagram looks like, let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure) As the pressure is lowered below that at A, the system eventually reaches a pressure where the liquid just begins to vaporizes (point D). At point D, the liquid has composition xlb where xlb at D is equal to the overall mole fraction xB since only an infinitesimal amount of liquid has vapourized. What is the composition of the first vapour that comes off ? Raoult's law, Pb=xvbPob relates the vapour-phase mole fractions to the liquid composition as follows:
Where Pob and Pocare the vapour pressures of pure 'B' and pure 'C' at T, where the system's pressure P equals the sum PB + Pc of the partial pressures, where and the vapor is assumed ideal.
Let B be the more volatile component, meaning that Pob>Poc Above equation then shows that Xvb/Xvc>Xlb/XlcThe vapor above an ideal solution is richer than the liquid in the more volatile component. Equations (1) and (2) apply at any pressure where liquid -vapor equilibrium exists, not just at point D.
Now let us isothermally lower the pressure below point D, causing more liquid to vaporize. Eventually, WE reach point F in figure, where the last drop of liquid vaporizes. Below F, we have only vapor. For any point or the line between D and F liquid and vapor phases coexist in equilibrium.
Q.
Two liquids A and B have the same molecular weight and form an ideal solution. The solution has a vapor pressure of 700 Torrs at 80°C. It is distilled till 2/3rd of the solution (2/3rd moles out of total moles) is collected as condensate.The composition of the condensate is x'A = 0.75 and that of the residue is X"A= 0.30. If the vapor pressure of the residue at 80°C is 600 Torrs, find the original composition of the liquid.
Colligative property measurement is one of the techniques used in the measurement of chemical quantities with reasonable accuracy.
If a 40.65 gm sample of K2SO4 and BaSO4 is dissolved in 900 gm of pure water to form a solution 'A' at 57°C, its vapour pressure is found to be 39.6 torr while vapour pressure of pure water at 57°C is 40 torr. Density of solution A is 1.24 gm/ml.
In a different experiment when small amount of pure BaSO4 is mixed with water at 57°C it gives the osmotic rise of 4.05 x 10-5 atm. (R = 0.082 Lt.-atm/mol-K ; K = 39, Ba = 137, S = 32, 0 = 16)
Percentage of K2SO4 in the sample is : .
Colligative property measurement is one of the techniques used in the measurement of chemical quantities with reasonable accuracy.
If a 40.65 gm sample of K2SO4 and BaSO4 is dissolved in 900 gm of pure water to form a solution 'A' at 57°C, its vapour pressure is found to be 39.6 torr while vapour pressure of pure water at 57°C is 40 torr. Density of solution A is 1.24 gm/ml.
In a different experiment when small amount of pure BaSO4 is mixed with water at 57°C it gives the osmotic rise of 4.05 x 10-5 atm. (R = 0.082 Lt.-atm/mol-K ; K = 39, Ba = 137, S = 32, 0 = 16)
Q.
Solubility product of BaSO4 in water at 57°C is : .
Colligative property measurement is one of the techniques used in the measurement of chemical quantities with reasonable accuracy.
If a 40.65 gm sample of K2SO4 and BaSO4 is dissolved in 900 gm of pure water to form a solution 'A' at 57°C, its vapour pressure is found to be 39.6 torr while vapour pressure of pure water at 57°C is 40 torr. Density of solution A is 1.24 gm/ml.
In a different experiment when small amount of pure BaSO4 is mixed with water at 57°C it gives the osmotic rise of 4.05 x 10-5 atm. (R = 0.082 Lt.-atm/mol-K ; K = 39, Ba = 137, S = 32, 0 = 16)
Q.
Concentration of Ba2+ ions in solution 'A' is : .
Colligative property measurement is one of the techniques used in the measurement of chemical quantities with reasonable accuracy.
If a 40.65 gm sample of K2SO4 and BaSO4 is dissolved in 900 gm of pure water to form a solution 'A' at 57°C, its vapour pressure is found to be 39.6 torr while vapour pressure of pure water at 57°C is 40 torr. Density of solution A is 1.24 gm/ml.
In a different experiment when small amount of pure BaSO4 is mixed with water at 57°C it gives the osmotic rise of 4.05 x 10-5 atm. (R = 0.082 Lt.-atm/mol-K ; K = 39, Ba = 137, S = 32, 0 = 16)
Q.
Boiling point of solution A is (Kb water = 0.54 K-kg/mol) :
A system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vaporizes to form a more disordered gas. When a solulte is present , there is additional contribution to the entropy of the liquid due to increase randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas.
Thus , a solute (non volatile) lowers the vapour pressure of a liquid, and hence a higher booing point of the solution
Similarly, the greater randomness of the solution opposes the tendency to freeze. In consequence, a lower the temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution . Elevation of B.Pt. ΔTband depression of F.Pt. ΔTf of a solution are the colligative properties which depend only on the concentration of particles of the solute, not their identity.For dilute solutions, ΔTb and ΔTf are proportional to the molality of the solute in the solution.
The vaues of Kb and Kf do depend on the properties of the solvent. For liquids, is almost constant .
[Troutan’s Rule , this constant for most of the Unassociated liquids (not having any strong bonding like Hydrogen bonding in the liquid state) is equal to 90J/mol. ]
For solutes undergoing change of molecular state is solution (ionization or association), the observed ΔT values differ from the calculate ones using the above relations. In such situations, the relationships are modified as
Where i = Van’t –Hoff factor, greater than unity for ionization and smaller than unity for association of the solute molecules.
Q.
Depression of freezing point of which of the following solutions does represent the cryoscopic constant of water?
A system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vaporizes to form a more disordered gas. When a solulte is present , there is additional contribution to the entropy of the liquid due to increase randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas.
Thus , a solute (non volatile) lowers the vapour pressure of a liquid, and hence a higher booing point of the solution
Similarly, the greater randomness of the solution opposes the tendency to freeze. In consequence, a lower the temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution . Elevation of B.Pt. ΔTband depression of F.Pt. ΔTf of a solution are the colligative properties which depend only on the concentration of particles of the solute, not their identity.For dilute solutions, ΔTb and ΔTf are proportional to the molality of the solute in the solution.
The vaues of Kb and Kf do depend on the properties of the solvent. For liquids, is almost constant .
[Troutan’s Rule , this constant for most of the Unassociated liquids (not having any strong bonding like Hydrogen bonding in the liquid state) is equal to 90J/mol. ]
For solutes undergoing change of molecular state is solution (ionization or association), the observed ΔT values differ from the calculate ones using the above relations. In such situations, the relationships are modified as
Where i = Van’t –Hoff factor, greater than unity for ionization and smaller than unity for association of the solute molecules.
Q.
Dissolution of a non-volatile solute into a liquid leads to the –
A system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vaporizes to form a more disordered gas. When a solulte is present , there is additional contribution to the entropy of the liquid due to increase randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas.
Thus , a solute (non volatile) lowers the vapour pressure of a liquid, and hence a higher booing point of the solution
Similarly, the greater randomness of the solution opposes the tendency to freeze. In consequence, a lower the temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution . Elevation of B.Pt. ΔTband depression of F.Pt. ΔTf of a solution are the colligative properties which depend only on the concentration of particles of the solute, not their identity.For dilute solutions, ΔTb and ΔTf are proportional to the molality of the solute in the solution.
The vaues of Kb and Kf do depend on the properties of the solvent. For liquids, is almost constant .
[Troutan’s Rule , this constant for most of the Unassociated liquids (not having any strong bonding like Hydrogen bonding in the liquid state) is equal to 90J/mol. ]
For solutes undergoing change of molecular state is solution (ionization or association), the observed ΔT values differ from the calculate ones using the above relations. In such situations, the relationships are modified as
Where i = Van’t –Hoff factor, greater than unity for ionization and smaller than unity for association of the solute molecules.
Q.
To aqueous solution of Nal, increasing amounts of solid HgI2 is added. The vapor pressure of the solution
A system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vaporizes to form a more disordered gas. When a solulte is present , there is additional contribution to the entropy of the liquid due to increase randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas.
Thus , a solute (non volatile) lowers the vapour pressure of a liquid, and hence a higher booing point of the solution
Similarly, the greater randomness of the solution opposes the tendency to freeze. In consequence, a lower the temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution . Elevation of B.Pt. ΔTband depression of F.Pt. ΔTf of a solution are the colligative properties which depend only on the concentration of particles of the solute, not their identity.For dilute solutions, ΔTb and ΔTf are proportional to the molality of the solute in the solution.
The vaues of Kb and Kf do depend on the properties of the solvent. For liquids, is almost constant .
[Troutan’s Rule , this constant for most of the Unassociated liquids (not having any strong bonding like Hydrogen bonding in the liquid state) is equal to 90J/mol. ]
For solutes undergoing change of molecular state is solution (ionization or association), the observed ΔT values differ from the calculate ones using the above relations. In such situations, the relationships are modified as
Where i = Van’t –Hoff factor, greater than unity for ionization and smaller than unity for association of the solute molecules.
Q.
A liquid possessing which of the following characteristics will be most suitable for determining the molecular mass of a compound by cryoscopic measurements?
A system of greater disorder of molecules is more probable. The disorder of molecules is reflected by the entropy of the system. A liquid vaporizes to form a more disordered gas. When a solulte is present , there is additional contribution to the entropy of the liquid due to increase randomness. As the entropy of solution is higher than that of pure liquid, there is weaker tendency to form the gas.
Thus , a solute (non volatile) lowers the vapour pressure of a liquid, and hence a higher booing point of the solution
Similarly, the greater randomness of the solution opposes the tendency to freeze. In consequence, a lower the temperature must be reached for achieving the equilibrium between the solid (frozen solvent) and the solution . Elevation of B.Pt. ΔTband depression of F.Pt. ΔTf of a solution are the colligative properties which depend only on the concentration of particles of the solute, not their identity.For dilute solutions, ΔTb and ΔTf are proportional to the molality of the solute in the solution.
The vaues of Kb and Kf do depend on the properties of the solvent. For liquids, is almost constant .
[Troutan’s Rule , this constant for most of the Unassociated liquids (not having any strong bonding like Hydrogen bonding in the liquid state) is equal to 90J/mol. ]
For solutes undergoing change of molecular state is solution (ionization or association), the observed ΔT values differ from the calculate ones using the above relations. In such situations, the relationships are modified as
Where i = Van’t –Hoff factor, greater than unity for ionization and smaller than unity for association of the solute molecules.
Q.
A mixture of two immiscible liquids at a constant pressure of 1 atm boils at a temperature
Assuming all the solutes are non volatile and all solutions are ideal
For a binary liquid solution of A and B. pAO = pure vapour pressure of A. pBO = pure
vapour pressure of B. XA = mole fraction of A in liquid phase. YA = mole fraction of in vapour phase.
Column —I Column—II

















