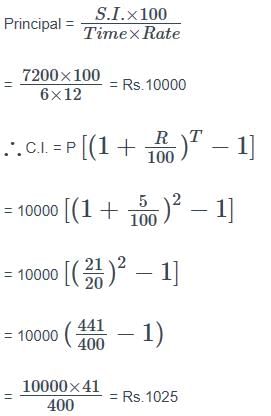Test: Simple Interest & Compound Interest- 2 - Quant MCQ
20 Questions MCQ Test - Test: Simple Interest & Compound Interest- 2
The simple interest accrued on a sum of certain principal is Rs. 6500/- in eight years at the rate of 13 p.c.p.a. What would be the compound interest accrued on that principal at the rate of 8 p.c.p.a. in 2 years?
The compound interest accrued on an amount of the end of two years @ 12 p.c.p.a. is Rs. 2862/- What is the amount?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The simple interest accrued on a sum of certain principal is Rs. 7,200/- in six years at the rate of 12 p.c.p.awhat would be the compound interest accrued on that principal at the rate of 5 p.c.p.a. in 2 years.
The simple interest accrued on a sum of certain capital principal is Rs. 6400/- in four years at the rate of 8 p.c.p.a. what would be the compound interest accrued on that principal at the rate of 2 p.c.p.a. in 2 years?
The simple interest accrued on an amount of Rs. 22,500/- at the end of four years is Rs. 10,800/-. What would be the compound interest accrued on the same amount at the same rate at the end of two years?
The simple interest accrued on an amount of Rs. 45000/- after 2 years at a certain rate of interest is 13500/-. What will be the compound interest accrued on the same amount in the same number years at the same rate of interest?
The simple interest accrued on a sum of certain principal is Rs. 2000/- in five years at the rate of 4 p.c.p.a. what would be the compound interest accrued on same principal at same rate in two years?
Ravi borrowed some money at the rate of 4 pcpa for the first three years, at the rate of 8 pcpa for the next two years and at the rate of 9 pcpa for the period beyond 5 years. If he pays a total simple interest of Rs. 19550 at the end of 7 years, how much money did he borrow?
A sum was put at simple interest at a certain rate for 5 years. had it been put at 5% higher rate, it would have fetched Rs. 500 more. What is the sum?
What is the difference between the compound interest and the simple interest for the sum Rs. 16000 at 5% p.a. for 2 years?
A sum of money doubles itself in 2 years at a simple interest. In how many years will it multiply four times?
A sum of money triples itself in 3 years at a simple interest. In how many years will it multiply five times?
An amount of money grows upto Rs. 4000 in 2 years and up to Rs. 8000 in 3 years on compound interest. What is the sum?
A man borrows Rs. 4000 and pays back after 5 years at 15% simple interest. The amount paid by the man is:
What is the time period for which Rs. 8000 amounts to Rs. 12000 at 20% p.a. of simple interest?
What is the rate of simple interest at which Rs. 14,000 gives interest of Rs. 1960 in two years?
What is the sum of amount which gives Rs. 6300 as interest @ 7% per annum of simple interest in 7*1/2years?
If the rate of simple interest is 12% per annum, the amount that would fetch interest of Rs. 6000 per annum is:
A sum was put at simple interest at a certain rate for 2 years. Had it been put at 4% higher rate, it would have fetched Rs. 112 more. The sum is:
In what time will a sum of money double itself @ 20% per annum (p.a.) simple interest?
Important Questions for Simple Interest & Compound Interest- 2
Simple Interest & Compound Interest- 2 MCQs with Answers
Online Tests for Simple Interest & Compound Interest- 2
|
© EduRev
|
Education Revolution
|
|
