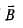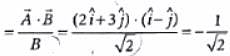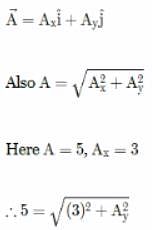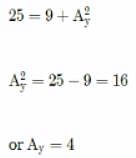Test: Resolution of Vectors (May 18) - JEE MCQ
10 Questions MCQ Test - Test: Resolution of Vectors (May 18)
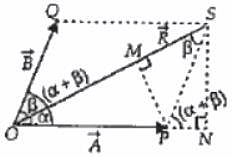
Two vectors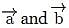 inclined at an angle θ have a resultant
inclined at an angle θ have a resultant which makes an angle α with
which makes an angle α with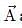 and angle β with
and angle β with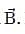 Let the magnitudes of the vectors
Let the magnitudes of the vectors  be represented by A, B and R respectively. Which of the following relations is not correct?
be represented by A, B and R respectively. Which of the following relations is not correct?
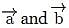 inclined at an angle θ have a resultant
inclined at an angle θ have a resultant which makes an angle α with
which makes an angle α with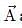 and angle β with
and angle β with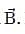 Let the magnitudes of the vectors
Let the magnitudes of the vectors  be represented by A, B and R respectively. Which of the following relations is not correct?
be represented by A, B and R respectively. Which of the following relations is not correct?| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If n is a unit vector in the direction of the vector 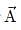 then
then
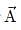 then
thenVectors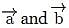 include an angle θ between them. If
include an angle θ between them. If respectively subtend angles α and β with
respectively subtend angles α and β with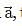 then (tanα + tanβ) is :
then (tanα + tanβ) is :
Which of the following quantities is dependent of the choice of orientation of the coordinate axes?
The components of Vector 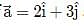 along the directions of vectors (
along the directions of vectors (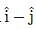 ) is
) is
A unit vector perpendicular to i^−2j^+k^ and 3i^−j^+2k^ is
The magnitude of the x-component of vector 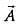 is 3 and the magnitude of vector
is 3 and the magnitude of vector 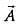 is 5. What is the magnitude of the y-component of vector
is 5. What is the magnitude of the y-component of vector 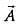 ?
?
If a vector 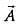 makes angles α, β and γ with X, Y and Z axes respectively then sin2α + sin2β + sin2γ is equal to
makes angles α, β and γ with X, Y and Z axes respectively then sin2α + sin2β + sin2γ is equal to
A unit vector in the direction of resultant vector of 


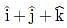 are
are 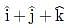 ∴ Ax = 1, Ay = 1, Az = 1
∴ Ax = 1, Ay = 1, Az = 1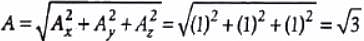
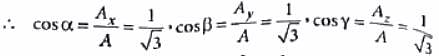
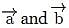 making an angle (α + β). Using the parallelogram method of vector addition,
making an angle (α + β). Using the parallelogram method of vector addition,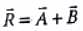
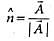
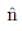 = unit vector
= unit vector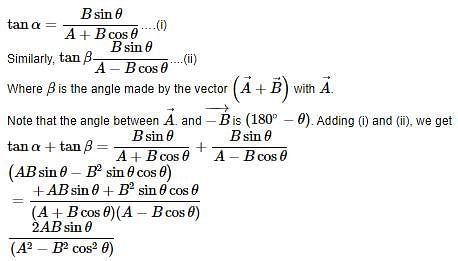
 angle between
angle between  are independent of the orientation of the coordinate axes. But the quantity Ax + By depends upon the magnitude of the components along x and y axes, so it will change with change in coordinate axes.
are independent of the orientation of the coordinate axes. But the quantity Ax + By depends upon the magnitude of the components along x and y axes, so it will change with change in coordinate axes.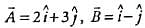 , (say) components of
, (say) components of