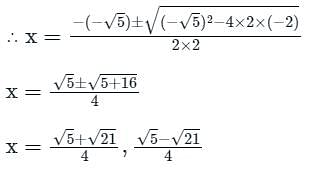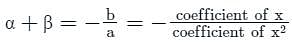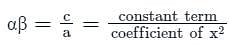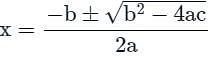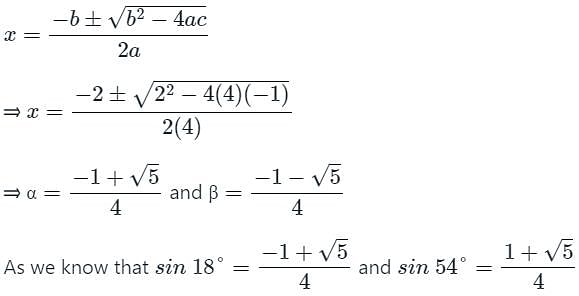Test: Quadratic Equations: Relation between Roots (June 7) - JEE MCQ
10 Questions MCQ Test - Test: Quadratic Equations: Relation between Roots (June 7)
If α, β are the roots of the equation x2 + x + 2 = 0, then what is 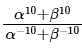 equal to?
equal to?
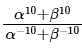 equal to?
equal to?If α and β are the zeros of the quadratic polynomial f (x) = x2 - 5x +6, find the value of ( α2β + β2α ).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Roots of the equation 2x2 - √5x - 2 = 0 are
If k is one of the roots of the equation x(x + 1) + 1 = 0, then what is its other root?
If α, β are the roots of the equation x2 + px + q = 0, then the value of α2 + β2
If α and β are zeroes of the polynomial x2 + 3x + 4, then find the value of α2 + β2.
4x2 + 8x – β = 0 has roots -5α and 3 .What is the value of β ?
If α and β are the zero of the polynomials fx = x2 + 5x + k satisfying the relation α2 + β2 − αβ = 22, then find the value of k for this to be possible.
If α and β are the roots of the equation 4x2 + 2x - 1 = 0, then which one of the following is correct?
If α and β are roots of the equation x2 + 5|x| - 6 = 0 then the value of |tan-1 α - tan-1 β| is