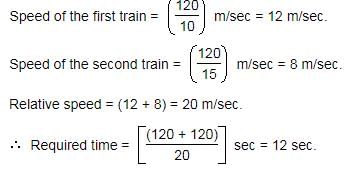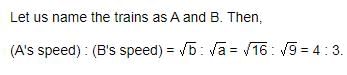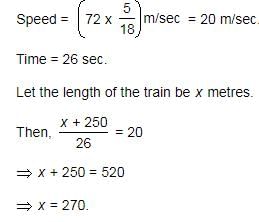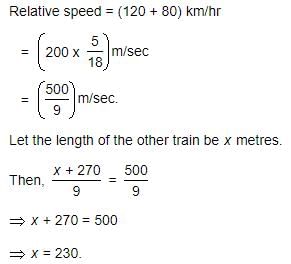All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  Test: Problems On Trains- 1 (May 27) - CAT MCQ

Test: Problems On Trains- 1 (May 27) - CAT MCQ


Test Description

10 Questions MCQ Test - Test: Problems On Trains- 1 (May 27)

Test: Problems On Trains- 1 (May 27) for CAT 2024 is part of CAT preparation. The Test: Problems On Trains- 1 (May 27) questions and answers have been prepared according to the CAT exam syllabus.The Test: Problems On Trains- 1 (May 27) MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Problems On Trains- 1 (May 27) below.
Solutions of Test: Problems On Trains- 1 (May 27) questions in English are available as part of our course for CAT & Test: Problems On Trains- 1 (May 27) solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: Problems On Trains- 1 (May 27) | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
Test: Problems On Trains- 1 (May 27) - Question 1
Save

A train passes a platform in 36 seconds. The same train passes a man standing on the platform in 20 seconds. If the speed of the train is 54 km/hr, The length of the platform is:

Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 1

Test: Problems On Trains- 1 (May 27) - Question 2
Save

A train moves past a post and a platform 264 m long in 8 seconds and 20 seconds respectively. What is the speed of the train?

Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 2

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Problems On Trains- 1 (May 27) - Question 3
Save

Two trains having equal lengths, take 10 seconds and 15 seconds respectively to cross a post. If the length of each train is 120 meters, in what time (in seconds) will they cross each other when traveling in opposite direction?

Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 3

Test: Problems On Trains- 1 (May 27) - Question 4
Save

Two trains, one from P to Q and the other from Q to P, start simultaneously. After they meet, the trains reach their destinations after 9 hours and 16 hours respectively. The ratio of their speeds is
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 4

Test: Problems On Trains- 1 (May 27) - Question 5
Save

A train having a length of 1/4 mile , is traveling at a speed of 75 mph. It enters a tunnel 3 ½ miles long. How long does it take the train to pass through the tunnel from the moment the front enters to the moment the rear emerges?
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 5

Test: Problems On Trains- 1 (May 27) - Question 6
Save

A train runs at the speed of 72 kmph and crosses a 250 m long platform in 26 seconds. What is the length of the train?
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 6

Test: Problems On Trains- 1 (May 27) - Question 7
Save

A train overtakes two persons who are walking in the same direction to that of the train at 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. What is the length of the train?
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 7

Test: Problems On Trains- 1 (May 27) - Question 8
Save

A train is traveling at 48 kmph . It crosses another train having half of its length , traveling in opposite direction at 42 kmph, in 12 seconds. It also passes a railway platform in 45 seconds. What is the length of the platform?
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 8

► Let the length of the train traveling at 48 kmph be 2x meters. 

► And length of the platform is y meters.

► Relative speed of train = (48+42) kmph

= (90*5/18) = 25 m/sec;

And 48 kmph = 48*5/18 = 40/3 m/sec.

 

► According to the question,

(2x +x)/25 = 12;

Or, 3x = 12*25 = 300;

Or, x = 300/3 = 100m 

► Then, length of the train = 2x = 100*2 = 200m.

200+y/(40/3) = 45;

600+3y = 40*45;

Or, 3y = 1800-600 = 1200;

Or, y = 1200/3 = 400 m.

► Length of the platform = 400 m.

Test: Problems On Trains- 1 (May 27) - Question 9
Save

A 270 metres long train running at the speed of 120 kmph crosses another train running in opposite direction at the speed of 80 kmph in 9 seconds. What is the length of the other train?
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 9

Test: Problems On Trains- 1 (May 27) - Question 10
Save

Two trains, each 100 m long are moving in opposite directions. They cross each other in 8 seconds. If one is moving twice as fast the other, the speed of the faster train is
Detailed Solution for Test: Problems On Trains- 1 (May 27) - Question 10

Information about Test: Problems On Trains- 1 (May 27) Page
In this test you can find the Exam questions for Test: Problems On Trains- 1 (May 27) solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Problems On Trains- 1 (May 27), EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for Problems On Trains- 1 (May 27)

Find all the important questions for Problems On Trains- 1 (May 27) at EduRev.Get fully prepared for Problems On Trains- 1 (May 27) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Problems On Trains- 1 (May 27) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Problems On Trains- 1 (May 27) resources.

Problems On Trains- 1 (May 27) MCQs with Answers

Prepare for the Problems On Trains- 1 (May 27) within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Problems On Trains- 1 (May 27)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Problems On Trains- 1 (May 27) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup