CAT Previous Year Questions: Number System (June 3) - CAT MCQ
10 Questions MCQ Test - CAT Previous Year Questions: Number System (June 3)
Let n be the least positive integer such that 168 is a factor of 1134n. If m is the least positive integer such that 1134n is a factor of 168m, then m + n equals [2023]
The number of all natural numbers up to 1000 with non-repeating digits is [2023]
For any natural numbers m, n , and k, such that k divides both m + 2n and 3m + 4n, k must be a common divisor of [2023]
The number of positive integers less than 50, having exactly two distinct factors other than 1 and itself, is [2023]
For any real number x, let |x| be the largest integer less than or equal to x. If 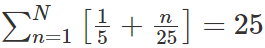 then N is [2022]
then N is [2022]
A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order? [2021]
For a 4-digit number, the sum of its digits in the thousands, hundreds and tens places is 14, the sum of its digits in the hundreds, tens and units places is 15, and the tens place digit is 4 more than the units place digit. Then the highest possible 4-digit number satisfying the above conditions is [2021]
Suppose one of the roots of the equation ax2 - bx + c = 0 is 2+ √3 , Where a,b and c are rational numbers and a ≠ 0. If b = c3 then | a | equals. [2021]