Test: Ray Optics & Optical Instruments - 1
30 Questions MCQ Test | Test: Ray Optics & Optical Instruments - 1
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Light from each point on a luminous object travels outward in all directions in straight lines. Light travels at very high speeds, but is not instantaneously everywhere. Light from a point object travels indefinitely until it collides with matter in its path to be partially absorbed and reflected.
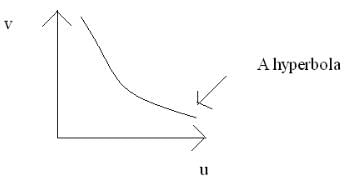
The graph drawn with object distance along abscissa & image as ordinate for a convex lens is
In a convex lens, (1/v)−(1/u)=(1/f)
Or (1/v)−(1/f)=(1/u) where u is always negative and f is always positive.
(1/v)=(1/f)−(1/u)
So, as u is increased 1/u will decrease and (1/f)−(1/u) will increase, so, 1/v increases or v decreases.
So, its graph will be a hyperbola
A lens of power + 2.0 D is placed in contact with another lens of power – 1.0 D. The combination will behave like
P=P1+P2=+2−1=+1 dioptre, lens behaves as convergent
F=1/P=1/1=1m=100cm
A short pulse of white light is incident from air to a glass slab at normal incidence. After travelling through the slab, the first colour to emerge is
In air, all the colours of light travel with the same velocity with the same velocity, but in glass, velocities of different colours are different. Velocity of red colour is largest and velocity of violet colour is smallest. Therefore, after travelling through the glass slab, red colour will emerge first.
According to Cartesian sign convention.
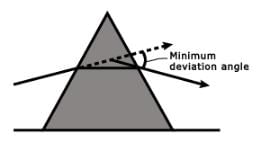
At the minimum deviation Dm, the refracted ray inside the prism
When the deviation is minimum, then the incidence angle and emergence angle are equal and this is possible only when the refracted ray inside the prism is parallel to the base of the prism.
Minimum deviation is given by δ=2i−A, where A is prism angle.
An observer looks at a tree of height 15 metre with a telescope of magnifying power 10. To him, the tree appears
Magnification of a telescope is given by:
M= θi/θo
10= (h/di)/(h/do)
10= do/di
Distance of image, di=do/10
Magnifying power of a compound microscope is high if
Magnifying power of a compound- microscope is given by m=− (lD/f0fe)
where, l is length of tube
D is least distance of clear vision
f0 is focal length of objective
fe is focal length of eyepiece
So, clearly, it can be seen that focal length of objective and eyepiece needs to be decreased so that magnifying power increases.
According to Cartesian sign convention the heights measured
The bluish color predominates in a clear sky,
The molecules of air and other fine particles in the atmosphere have a size smaller than the wavelength of visible light. These particles are more effective in scattering light of a shorter wavelength at the blue end than the light of the longer wavelengths at the red end. The red light has a wavelength 1.8 times greater than blue light. Thus, when sunlight passes through the atmosphere, the fine particles in the air scatter the blue color more strongly than red color. The scattered blue light enters our eyes and we see the blue color of the clear sky.
The magnifying power of the telescope can be increased by
Magnifying power of a telescope is f0/fe , so as 1/fe increases, magnifying power increases.
Hence the correct answer is option D.
A lamp and a screen are set up 100 cm apart and a convex lens is placed between them. The two positions of the lens forming real images on the screen are 40 cm apart. What is the focal length of the lens ?
L1L2=40cm and O I=100cm
Therefore, x+40+x=100 or x=30cm
For lens at L1, we have
U=-30cm and v=+70
Thus,
(1/v)-(1/u)=1/f
Or, 1/f=(1/70) - (1/-30)
Or, f=+21cm
The magnifying power of telescope is high if
The ability of the eye lens to adjust its focal length is called power of accommodation. This is done by the ciliary muscles by changing the focal length of the eye lens.
The largest telescope in the world has a reflector with an aperture of 200 inches in order to achieve
A convex lens forms a real image of an object on a screen; the magnification of the image being 3/2. The object and the screen are kept fixed and the lens is moved through a distance of 16 cm when a sharp image is again formed on the screen; the magnification now being 2/3. What is the focal length of the lens?
3/2=v/u…...1
2/3=(v-16)/(u+16)......2
from these equation
we get v=48, u=32
so now f=(vxu)/(v+u)=96/5=19.2
The correct answer is option B.
A plano-convex lens, when silvered on the plane side, behaves like a concave mirror of focal length 30 cm. When it is silvered on the convex side, it behaves like a concave mirror of focal length 10 cm. The refractive index of the material of the lens is
Given: A plano-convex lens when silvered on the plane side behaves like a concave mirror of focal length 60cm. However, when silvered on the convex side, it behaves like a concave mirror of focal length 20cm.
To find the refractive index of the lens
We know,
1/F=(2/f)+(1/fm)............(i), where
When plane surface is silvered it becomes concave mirror of focal length 60cm,
and fm=∞
So the eqn(i) becomes,
1/60=(2/f)+(1/∞)
⟹f=120cm
When convex side is silvered it becomes concave mirror of focal length 10cm,
and fm=R/2
So the eqn(i) becomes,
1/20=2/f+2/R
⟹2/R=(1/20)−(2/f)
⟹2/R=(1/20)−(2/120)
⟹2/R=(6−2/120)
⟹R=60cm
Now using the focal length formula of the plano-convex lens, we get
1/f=(μ−1)×1/R
⟹1/120=(μ−1)×1/60
⟹μ−1=(60/120)
⟹μ=(1/2)+1
⟹μ=1.5
is the refractive index of the lens.
For a rectangular slab, refraction takes place at
The refraction takes place at both the air-glass interface and glass-air interface of a rectangular glass slab. When the light ray incident on the air-glass interface (DC) obliquely, it bends towards the normal.
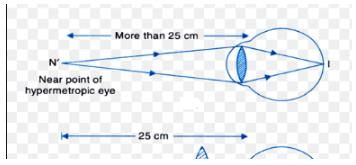
Farsighted or hypermetropic eye can be corrected by
Hypermetropia is corrected using converging lens. In this defect the person is able to see far objects clearly but difficulty with near vision. The image is focused behind the retina rather than upon it. This occurs when eyeball is too short or the power of lens is too weak. By using a convex lens the defect is corrected.
A Plano convex lens of curvature of 30 cm & R.I. 1.5, produces a real image of an object kept 90cm from it. The magnification is
We have, (1/v)−(1/−90)=1/f⇒(1.5−1)(1/30)=1/60
∴ v=180 cm
∴|m|=∣v/u∣=180/90=2.0
How will the image formed by a convex lens be affected if the central portion of the lens is wrapped in a black paper
An object is placed at a distance of 10 cm from a co-axial combination of two lenses A and B in contact. The combination forms a real image three times the size of the object. If lens B is concave with a focal length of 30 cm, what is the nature and focal length of lens A ?
A converging lens is used to form an image on a screen. When the upper half of the lens is covered by an opaque screen
The only difference in covering any part of a lens is that the intensity of the image will reduce. Since the focal length is a function of curvature of the surfaces of the lens and covering a part does not change it, the image will be formed as usual.
Total internal reflection can take place only if light is travelling from
An equi-convex thin lens (μ =1.5) of focal length in air as 30cm is sealed into an opening in one end of tank filled with water ((μ =1.33). At the end of the tank opposite the lens is a plane mirror, 80 cm distant from the lens. The position of the image formed by the lens-water-mirror system of a small object outside the tank on the lens axis and 90cm to the left of the lens will be
Optical fibre communication uses the principle of
According to Cartesian sign convention.
When an astronomical telescope is focused on a distant star, the distance of the eye piece from the objective is 60 cm. When focused on a distant flag post the eye piece must be drawn at 0.1cm. If the focal length of the eye piece is 5cm; what will be the distance of the pole from the objective? Assume that the eye is focused for infinity?
The objective of a telescope has a focal length of 1.2 m. It is used to view a 10.0 m tall tower 2 km away. What is the height of the image of the tower formed by the objective?
α (Radian)=10/2000=1/200rad
α=h/F=h/1.2
h= α x 1.2
h=(1/200) x1.2 cm
=6mm
Download free EduRev App
(Scan QR code)
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
