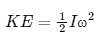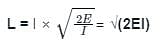Test: Rotational Work and Energy - EmSAT Achieve MCQ
10 Questions MCQ Test - Test: Rotational Work and Energy
A thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. The velocity of the other end when it hits the fioor, assuming that the end which is on the floor does not slip, will be :
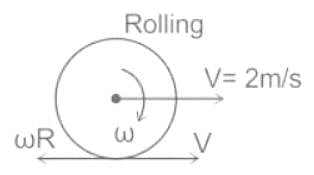
A thin ring of mass 10 kg is rolling on the horizontal ground such that its center of mass has a velocity of 2 m/s. How much work (in joules) needs to be done to stop it?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
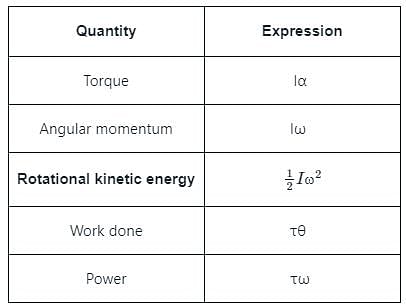
The product of torque and angular displacement is __________.
If a body is rolling down from a hill at certain height, the body will have
The work done to increase the velocity of a 1500 kg car from 36 km/h to 72 km/h is
A solid cylinder of mass 10 kg and radius 0.5 m is rotating about its axis at 20 rad/s. How much is it's kinetic energy (in joules)?
The bullet fired from a gun possesses which form of energy, that can pierce a target?
The expression Iω2/2 represents Rotational ____________
Moment of inertia, rotational kinetic energy, and angular momentum of a body is I, E, and L respectively then :
Two discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is


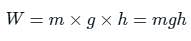


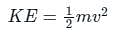
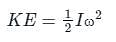
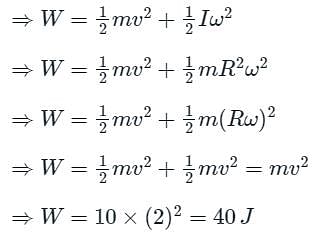

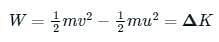
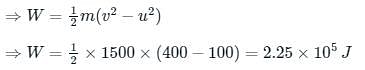
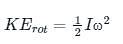
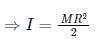

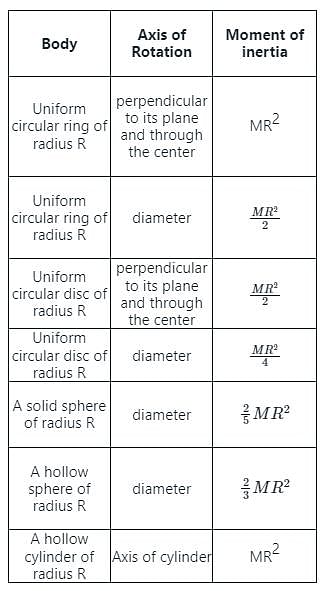
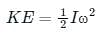
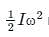 represents rotational kinetic energy.
represents rotational kinetic energy.