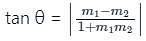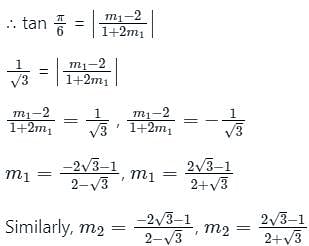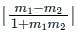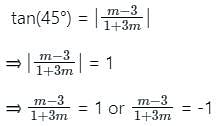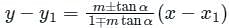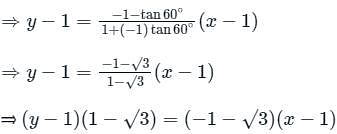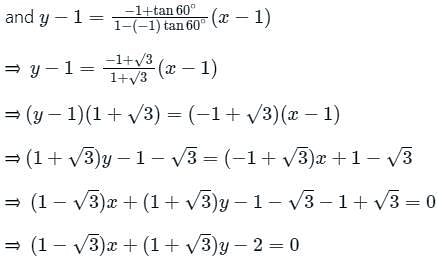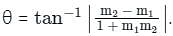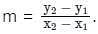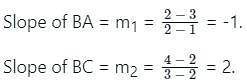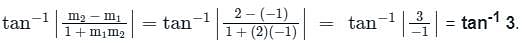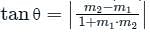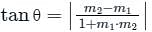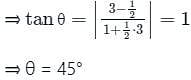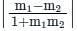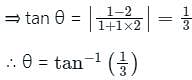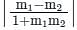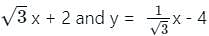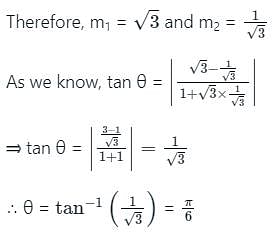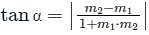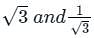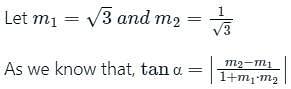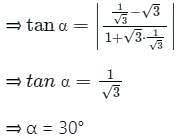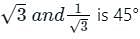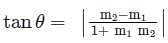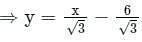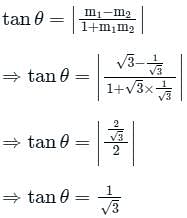Test: Straight Lines: Angle between Lines (6 July) - JEE MCQ
10 Questions MCQ Test - Test: Straight Lines: Angle between Lines (6 July)
The slope of a line L is 2. If m1, m2 are slopes of two lines which are inclined at an angle of (π/6) with L, then m1 + m2 =
The slopes of the lines which make an angle of 45° with the line 3x - y + 4 = 0 are
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The equation of a line making an angle 60° with the line x + y - 3 = 0 and passing through the point (1, 1) is
A triangle is formed by joining the three points A(1, 3), B(2, 2) and C(3, 4). The value of angle B will be:
Find the angle between the lines whose slopes are 1/2 and 3 ?
The acute angle between two lines y = x + 4 and y = 2x - 3 is
The acute angle between two lines y = 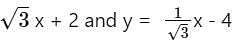 is
is
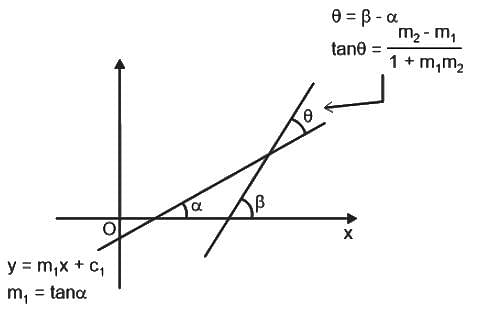
Find the angle between the lines whose slopes are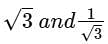
The angle between the lines 2x - y = 3 and x - 2y = 3 is
What is the acute angle between the lines represented by the equations