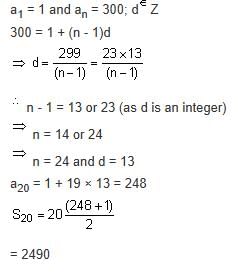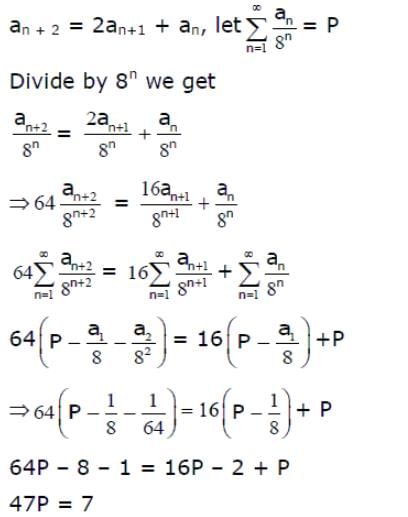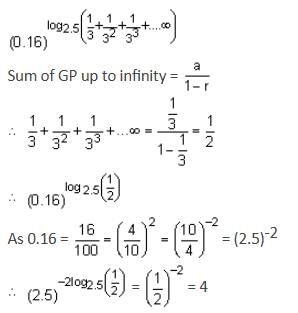Math Unit Test: Sequences & Series(June 20) - JEE MCQ
15 Questions MCQ Test - Math Unit Test: Sequences & Series(June 20)
Three numbers are in an increasing geometric progression with common ratio r. If the middle number is doubled, then the new numbers are in an arithmetic progression with common difference d. If the fourth term of GP is 3r2, then r2 - d is equal to:
If tan , x, tan
, x, tan are in arithmetic progression and tan
are in arithmetic progression and tan , y, tan
, y, tan are also in arithmetic progression, then |x - 2y| is equal to:
are also in arithmetic progression, then |x - 2y| is equal to:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The sum of all 3-digit numbers less than or equal to 500, that are formed without using the digit ''1'' and are multiples of 11, is __________. (in integer)
Let Sn denote the sum of first n terms of an arithmetic progression. If S10 = 530, S5 = 140, then S20 - S6 is equal to:
Let 3, 6, 9, 12, ... upto 78 terms and 5, 9, 13, 17, ... upto 59 terms be two series. Therefore, the sum of the terms common to both the series is equal to ___. (in integer)
The sum of 10 terms of the series + ... is:
Let an be the nth term of a G.P. of positive terms. If  = 200 and
= 200 and  = 100, then
= 100, then  is equal to:
is equal to:
Let a1, a2, ... an be a given A.P. whose common difference is an integer and Sn = a1 + a2 + ... + an. If a1 = 1, an = 300 and 15 n
50, then the ordered pair (Sn - 4, an - 4) is equal to
Let be a sequence such that a1 = 1, a2 = 1 and an + 2 = 2an + 1 + an for all n
1. Then the value of 47
is equal to __________. (in integer)
Let S1 be the sum of first 2n terms of an arithmetic progression. Let S2 be the sum of first 4n terms of the same arithmetic progression. If (S2 - S1) is 1000, then the sum of the first 6n terms of the arithmetic progression is equal to:
If , then the remainder when K is divided by 6 is
If (r3 + 6r2 + 2r + 5) =
(11!), then value of
is equal to ________. (in integer)
The greatest positive integer k, for which 49k + 1 is a factor of the sum 49125 + 49124 + ... + 492 + 49 + 1, is
The value of (0.16)log2.5 is equal to ________. (in integer)
If the sum of the first ten terms of the series is
, where m and n are co-prime numbers, then m + n is equal to ___________. (in integer)



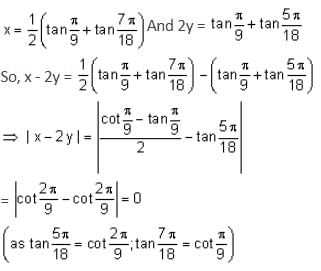

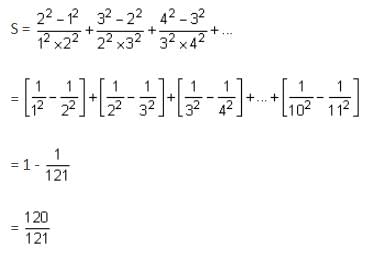
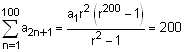 ... (i) and
... (i) and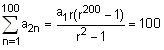 ... (ii)
... (ii)