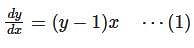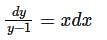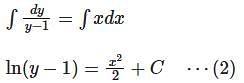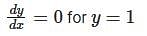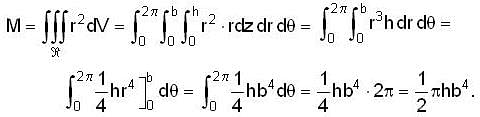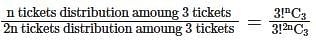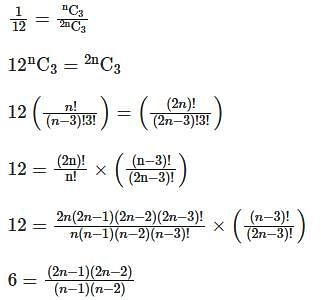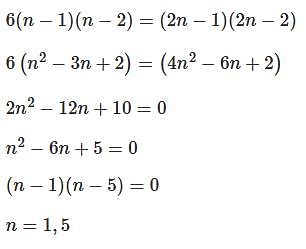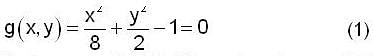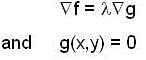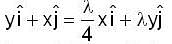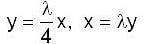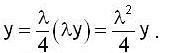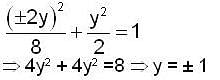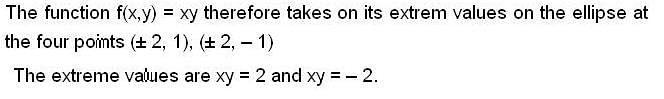IIT JAM Mathematics Mock Test- 1 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Mock Test- 1
Consider the differential equestion 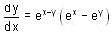 and y = 0 and x → ∞ then
and y = 0 and x → ∞ then 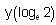 is
is
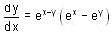 and y = 0 and x → ∞ then
and y = 0 and x → ∞ then 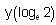 is
is| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Solution of the following differential equation 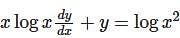 .
.
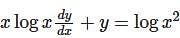 .
.Let T : R3 R3 be the linear transformation such that Y (1, 0, 1) = (0, 1, -1) and T(2, 1, 1) = (3, 2, 1) Then T(-1, -2, 1)
Choose a number n uniformly at random from the set {1,2,…,100}. Choose one of the first seven days of the year 2014 at random and consider n consecutive days starting from the chosen day. What is the probability that among the chosen �� days, the number of Sundays is different from the number of Mondays?
Let p(x) be a non-zero polynomial of degree N the radius of convergence of the power series 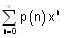
Let T: R2 → R3 be the Linear transformation whose matrixwith respect to standard basis of R3 and R2 is  The T
The T
Let 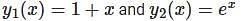 be two solutions of
be two solutions of 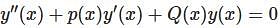 then the set of initial conditions for which the above differential equation has No solution is:
then the set of initial conditions for which the above differential equation has No solution is:
In an elastic collision of two particles, the following is conserved:
The solutions sin x and cos x of the differential equation 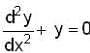 are
are
The least number which when divided by 4,5,6 and 7 leaves 3 as remainder, but when divided by 9 leaves no remainder is:
Which one of the following is the differential equation that represents the family of curves 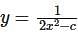 where c is an arbitrary constant?
where c is an arbitrary constant?
Let V be the vector space of real polynomials of degree atmost 2.which defines a linear operator 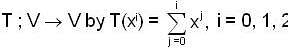 then the matrix of with respect to the basis (1 , x, x2) is
then the matrix of with respect to the basis (1 , x, x2) is
Value of the 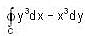 is (where C are the Wvo circles of radius 2 and 1 centered at the origin with positive orientation.)
is (where C are the Wvo circles of radius 2 and 1 centered at the origin with positive orientation.)
The equation of the curve which passes through the point (2a, a) and for which the sum of the Cartesian sub tangent and the abscissa is equal to the constant a, is:
The function sinx(1 + cosx) have maximum value at:
Which one of the following options contains two solutions of the differential equation 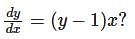
The mass of a solid right circular cylinder of height h and radius of base b, if density (mass per unit volume) is numerically equal to the square of the distance from the axis of the cylinder.is
Two different families A and B are blessed with an equal number of children. There are 3 tickets to be distributed amongst the children of these families so that no child gets more than one ticket. If the probability that all the tickets go to the children of the family B is 1 / 12, then the number of children in each family is :
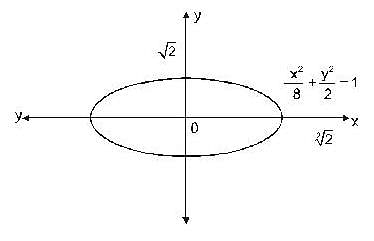
Using the method of Lagrange multipliers the greatest and smallest value that the function f (x, y) = xy takes on the ellipse 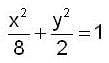 is
is


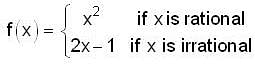
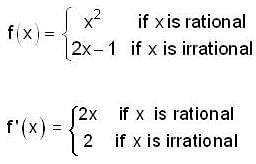
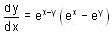
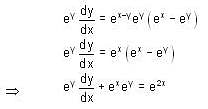
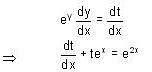
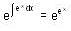
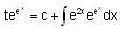
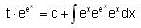
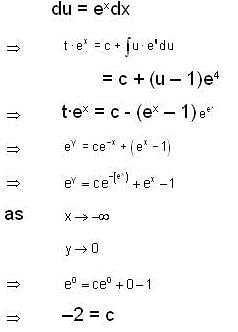
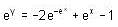
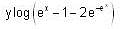
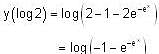
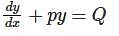
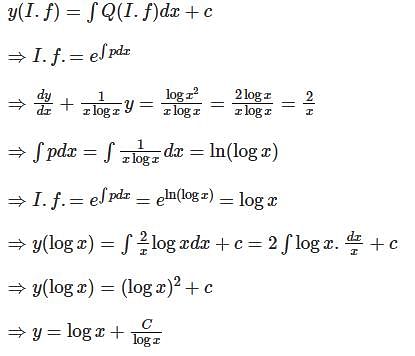
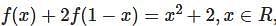 , then f(x) is given by-
, then f(x) is given by-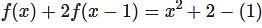
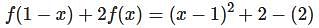
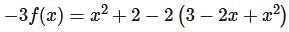
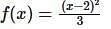
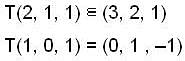
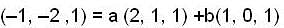
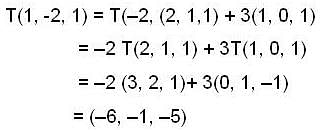
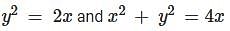
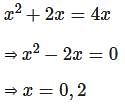

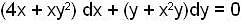 is
is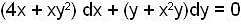
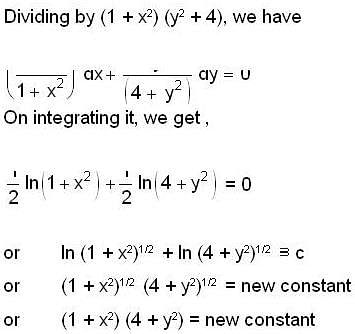
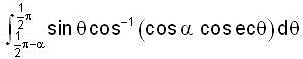 .
.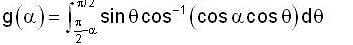
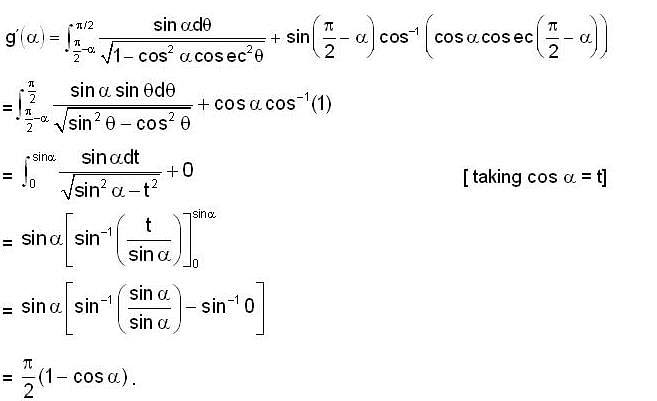
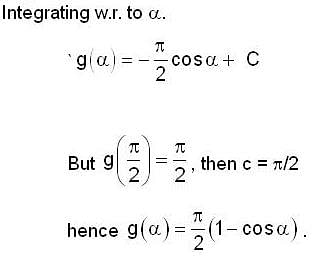
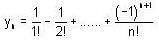
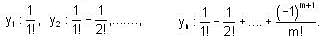
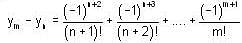
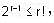 , it follows that if m > n, then
, it follows that if m > n, then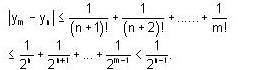
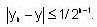
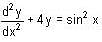 is given by;
is given by;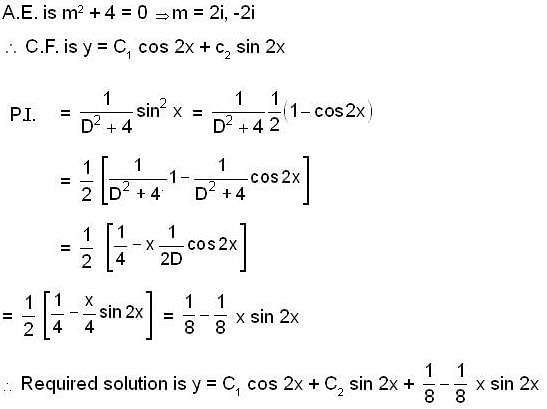
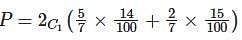
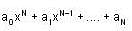


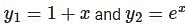 be two solutions of,
be two solutions of,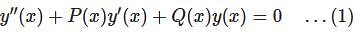
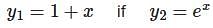
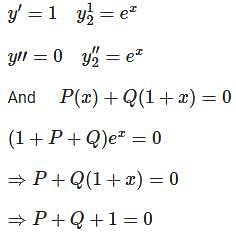
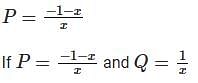
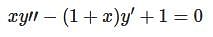
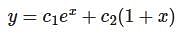
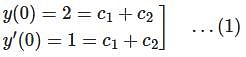
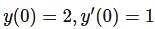 differential equation has no solution.
differential equation has no solution.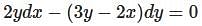 is:
is: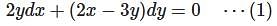
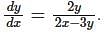
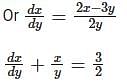
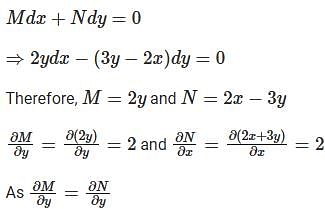
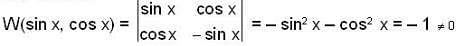
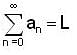 and if
and if 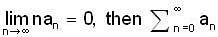 is
is
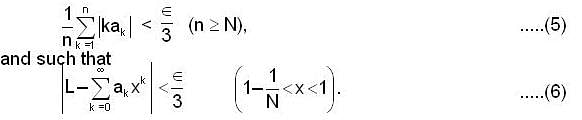
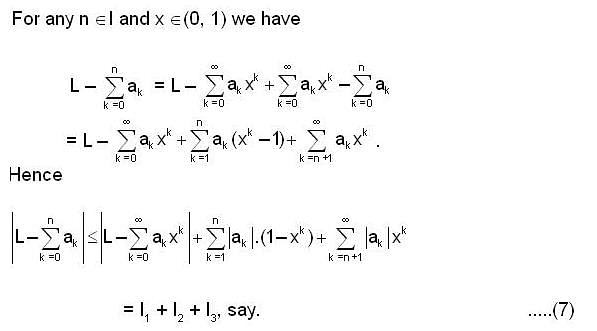
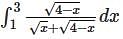
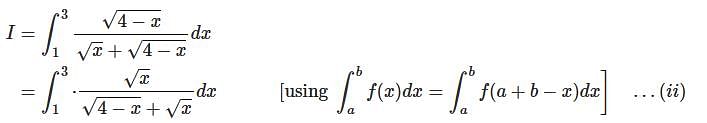
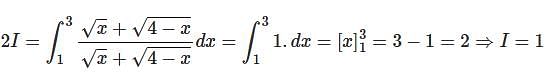
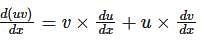
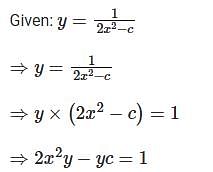
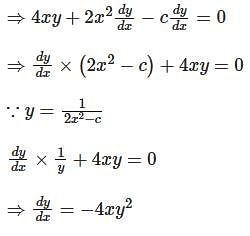
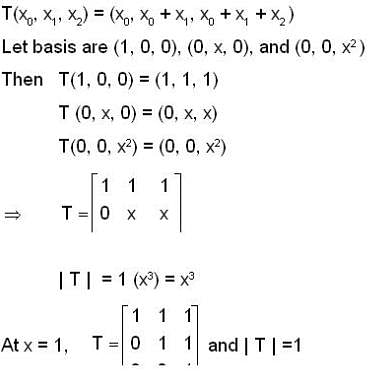

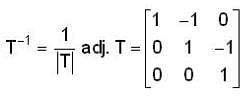
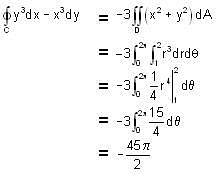
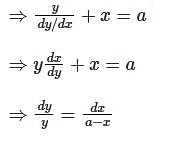
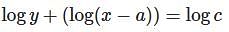
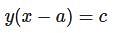
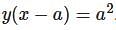 .
.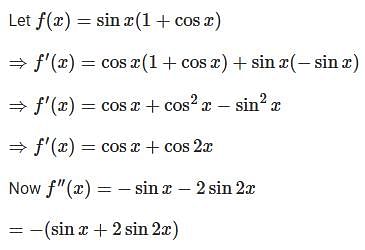
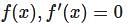
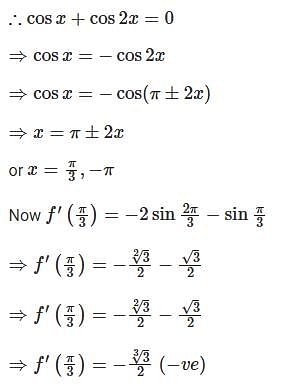
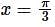 .
.