Interview Preparation Exam > Interview Preparation Tests > Practice Test: Number System- 3 - Interview Preparation MCQ
Practice Test: Number System- 3 - Interview Preparation MCQ
Test Description
20 Questions MCQ Test - Practice Test: Number System- 3
Practice Test: Number System- 3 for Interview Preparation 2025 is part of Interview Preparation preparation. The Practice Test: Number System- 3 questions and answers have been prepared
according to the Interview Preparation exam syllabus.The Practice Test: Number System- 3 MCQs are made for Interview Preparation 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Practice Test: Number System- 3 below.
Solutions of Practice Test: Number System- 3 questions in English are available as part of our course for Interview Preparation & Practice Test: Number System- 3 solutions in
Hindi for Interview Preparation course.
Download more important topics, notes, lectures and mock test series for Interview Preparation Exam by signing up for free. Attempt Practice Test: Number System- 3 | 20 questions in 40 minutes | Mock test for Interview Preparation preparation | Free important questions MCQ to study for Interview Preparation Exam | Download free PDF with solutions
Practice Test: Number System- 3 - Question 1
Raju had to divide 1080 by N, a two-digit number. Instead, he performed the division using M, which is obtained by reversing the digits of N, and ended up with a quotient that was 25 less than what he should have obtained otherwise. If 1080 is exactly divisible by both N and M, find the sum of the digits of N.
Detailed Solution for Practice Test: Number System- 3 - Question 1
Practice Test: Number System- 3 - Question 2
A rectangular floor is fully covered with square tiles of identical size. The tiles on the edges are white and the tiles in the interior are red. The number of white tiles is the same as the number of red tiles. What is a possible value of the number of tiles along one edge of the floor?
Detailed Solution for Practice Test: Number System- 3 - Question 2
Practice Test: Number System- 3 - Question 3
The sum of the factorials of the digits of a 3-digit number is equal to the 3-digit number formed by these digits, taken in the same order. Which of the following statements is true regarding the number of such 3-digit numbers, assuming no digit occurs more than once?
Detailed Solution for Practice Test: Number System- 3 - Question 3
Practice Test: Number System- 3 - Question 4
Let S be a two-digit number such that both S and S² end with the same digit and none of the digits in S equals zero. When the digits of S are written in reverse order, the square of the new number has a last digit of 6 and is less than 3000. How many values of S are possible?
Detailed Solution for Practice Test: Number System- 3 - Question 4
Practice Test: Number System- 3 - Question 5
Let N be a positive integer not equal to 1. Then none of the numbers 2, 3, ..., N is a divisor of (N! - 1). Thus, we can conclude that:
Detailed Solution for Practice Test: Number System- 3 - Question 5
Practice Test: Number System- 3 - Question 6
16 students were writing a test in a class. Rahul made 14 mistakes in the paper, which was the highest number of mistakes made by any student. Which of the following statements is definitely true?
Detailed Solution for Practice Test: Number System- 3 - Question 6
Practice Test: Number System- 3 - Question 7
What is the remainder when (10^3 + 9^3)^752 is divided by 123?
Detailed Solution for Practice Test: Number System- 3 - Question 7
Practice Test: Number System- 3 - Question 8
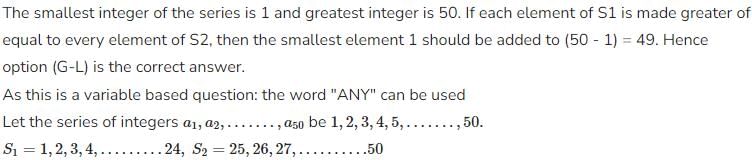
Every element of S1 is made greater than or equal to every element of S2 by adding an integer x to each element of S1. What is the minimum value that x can take?
Detailed Solution for Practice Test: Number System- 3 - Question 8
Practice Test: Number System- 3 - Question 9
The History teacher was referring to a year in the 19th century. Rohan found an easy way to remember the year. He found that the number, when viewed in a mirror, increased 4.5 times. Which year was the teacher referring to?
Detailed Solution for Practice Test: Number System- 3 - Question 9
Practice Test: Number System- 3 - Question 10
N is a number that, when divided by 10, gives 9 as the remainder; when divided by 9, gives 8 as the remainder; when divided by 8, gives 7 as the remainder; when divided by 7, gives 6 as the remainder; when divided by 6, gives 5 as the remainder; when divided by 5, gives 4 as the remainder; when divided by 4, gives 3 as the remainder; when divided by 3, gives 2 as the remainder; and when divided by 2, gives 1 as the remainder. What is N?
Detailed Solution for Practice Test: Number System- 3 - Question 10
Practice Test: Number System- 3 - Question 11
How many different four-digit numbers are there in the octal (Base 8) system, expressed in that system?
Detailed Solution for Practice Test: Number System- 3 - Question 11
Practice Test: Number System- 3 - Question 12
A teacher wrote a four-digit number on the blackboard, and the following observations were made by the students: The sum of the digits equals the product of the digits. Additionally, the number is divisible by the sum of the digits. What is the sum of the digits of the number?
Detailed Solution for Practice Test: Number System- 3 - Question 12
Practice Test: Number System- 3 - Question 13
Find the unit digit of the expression: 346^765 * 768^983 * 987^599.
Detailed Solution for Practice Test: Number System- 3 - Question 13
Practice Test: Number System- 3 - Question 14
A certain number when successively divided by 4, 5, and 7 leaves remainders 2, 3, and 5 respectively. Find the least such number.
Detailed Solution for Practice Test: Number System- 3 - Question 14
Practice Test: Number System- 3 - Question 15
A number when divided by 841 gives a remainder of 87. What will be the remainder when we divide the same number by 29?
Detailed Solution for Practice Test: Number System- 3 - Question 15
Practice Test: Number System- 3 - Question 16
A number when divided by 48 leaves a remainder of 31. Find the remainder when the same number is divided by 24.
Detailed Solution for Practice Test: Number System- 3 - Question 16
Detailed Solution for Practice Test: Number System- 3 - Question 17
Practice Test: Number System- 3 - Question 18
A number when divided by 703 gives a remainder of 75. What will be the remainder when we divide the same number by 37?
Detailed Solution for Practice Test: Number System- 3 - Question 18
Practice Test: Number System- 3 - Question 19
The product of two positive numbers is 616. If the ratio of the difference of their cubes to the cube of their difference is 157:3, then the sum of the two numbers is
Detailed Solution for Practice Test: Number System- 3 - Question 19
Practice Test: Number System- 3 - Question 20
The digits of a three-digit number A are written in the reverse order to form another three-digit number B. If B > A and B-A is perfectly divisible by 7, then which of the following is necessarily true?
Detailed Solution for Practice Test: Number System- 3 - Question 20
Information about Practice Test: Number System- 3 Page
In this test you can find the Exam questions for Practice Test: Number System- 3 solved & explained in the simplest way possible.
Besides giving Questions and answers for Practice Test: Number System- 3, EduRev gives you an ample number of Online tests for practice
Download as PDF