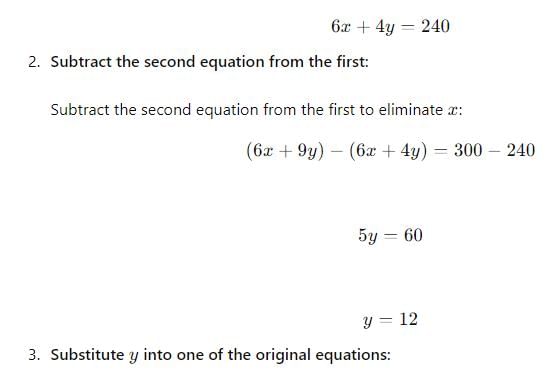CTET Practice Test: Mathematics - 2 - CTET & State TET MCQ
30 Questions MCQ Test - CTET Practice Test: Mathematics - 2
Letter ‘T’ of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about.
What is the number of integral solutions of the equation 2x2 – 3x – 2 = 0?
How do we write 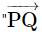 is perpendicular to
is perpendicular to 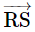 '' symbolically?
'' symbolically?
The following pictograph shows the number of absentees in a class of 30 students during the previous week. Which day had full attendance?

A bag has ₹ 785 in the denomination of ₹ 2, ₹ 5 and ₹ 10 coins. The coins are in the ratio of 6 : 9 : 10. How many coins of ₹ 5 are in the bag?
D and E are the mid-points of the sides AB and AC of △ABC and O is any point on the side BC, O is joined to A. If P and Q are the mid-points of OB and OC res, Then DEQP is
D and E are the mid-points of the sides AB and AC. Of △ABC. If BC = 5.6cm, find DE.
The incomes of Sheldon, Leonard, and Howard are in the ratio of 4 : 5 : 6 respectively and their spending are in the ratio of 6 : 7 : 8 respectively. If Sheldon saves one fourth his income, then the savings of Sheldon, Leonard, and Howard are in the ratio:
When a body falls freely under gravity, the distance d covered by it in time t is given by the formula:
, where g is a constant called acceleration due to gravity.
When a ball is dropped from a 16-feet high structure on earth, it takes 1 second to reach the ground. How much time will it take for a ball to reach the ground if it is dropped from a height of 2800 feet on a planet whose acceleration due to gravity is seven times that of earth?
Two numbers such that the sum of twice the first number and thrice the second number is 100 and the sum of thrice the first number and twice the second number is 120. Which is larger number?
If 1 is added to the greatest 7- digit number, it will be equal to
In the adjoining figure, the measure Of PR is
The formula for finding total surface area of cylinder is
Three Statements are given below:
(I) In a, Parallelogram the angle bisectors of 2 adjacent angles enclose a right angle.
(II) The angle bisector of a Parallelogram form a Rectangle.
(III) The Triangle formed by joining the mid-points of the sides of an isosceles triangle is not necessarily an isosceles triangle. Which is True?
Two parallelogram stand on equal bases and between the same parallels. The ratio of their areas is
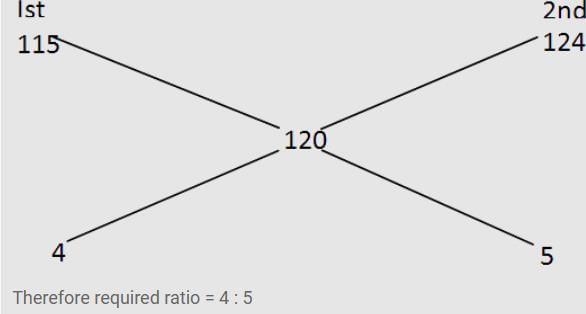
In what ratio must two kinds of sugar at Rs. 1.15 and Rs. 1.24 per kg be mixed so that by selling at Rs. 1.50 per kg, 25% may be gained
In addition and subtraction of the integers the sign of answer depends upon
If integers p, q and r are the roots of the equation x3-7x2+12x = 0, and p < q < r, what is the value of ?
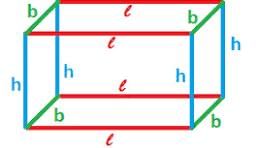
The formula for lateral surface area of cuboid is
The colours of fridges preferred by people living in a locality are shown by the following pictograph. Find the number of people preferring white colour.

In the given figure, perimeter of quadrilateral ABCD is
Keeping the place of 6 in the number 6350947 same, the smallest number obtained by rearranging other digits is
Find the number of lines of symmetry in the below figure: