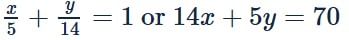Test: Linear Inequalities One Variable - JEE MCQ
15 Questions MCQ Test - Test: Linear Inequalities One Variable
If 3x + 22x ≥ 5x, then the solution set for x is:
x - 1)(x² - 5x + 7) < (x - 1), then x belongs to
The number of real solutions (x, y, z, t) of simultaneous equations: 2y = 11/x, 2z = 11/y, 2x = 11/z, 2x = 11/t
The solution set contained in R of the inequality 3x + 31-x - 4 < 0 is:
If 5x + (2√3) 2x ≥ 13x, then the solution set for x is:
The solution of inequality 4x + 3 < 5x + 7 when x is a real number is
Solution set of inequality loge((x - 2) / (x - 3)) is:
By solving the inequality 6x - 7 > 5, the answer will be
Let f(x) = ax² + bx + c and f(-1) < 1, f(1) > -1, f(3) < -4 and a ≠ 0, then:
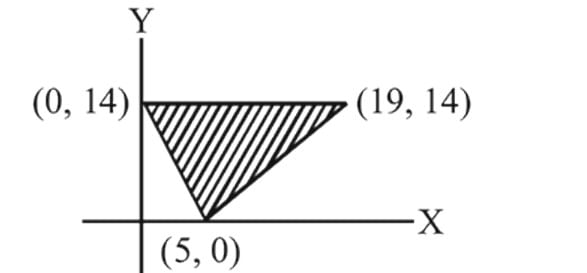
The shaded region shown in the figure is given by the inequations
The set of admissible values of x such that (2x + 3) / (2x - 9) < 0 is:
The number of real values of parameter k for which (log16x)2−log16x+log16k=0 will have exactly one solution is