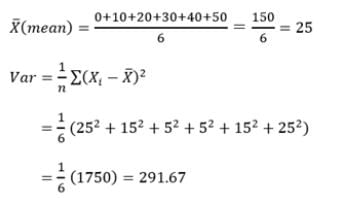Test: Variance And Standard Deviation - JEE MCQ
10 Questions MCQ Test - Test: Variance And Standard Deviation
Mean of the squares of the deviations from mean is called the:
The mean weight of a group of 10 items is 28 and that of another group of n items is 35.The mean of combined group of 10 + n items is found to be 30. The value of n is
A batsman scores runs in 10 innings as 38,70,48,34,42,55,63,46,54 and 44 , then the mean score is
For a given data, the standard deviation is 20.If 3 is added to each observation , what is the new variance of the resulting observations?
For a given data, the variance is 15. If each observation is multiplied by 2, what is the new variance of the resulting observations?
The following values are calculated in respect of marks of the students of sections A and B of Class X:
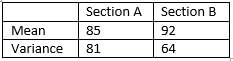
The marks of which section have more variability?
If  is large, there is a ______ degree of dispersion.
is large, there is a ______ degree of dispersion.
The standard deviation for the following data:

The standard deviation of first 10 multiples of 4 is: