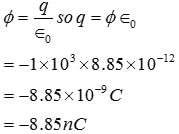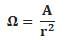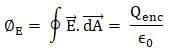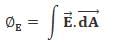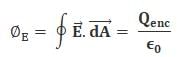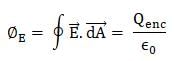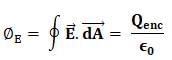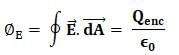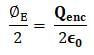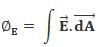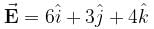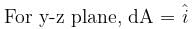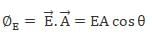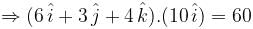Test: Electric Flux & Gauss Law - JEE MCQ
20 Questions MCQ Test - Test: Electric Flux & Gauss Law
If the electric field is given by 26i – k. Calculate the electric flux through a surface of area 20 units lying in x-y plane.
A point charge of 2.0 μC is at the center of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Electric flux through an area dA for an electric field E is given by:
A point charge causes an electric flux of −1.0×103 Nm2/C to pass through a spherical Gaussian surface of 10.0 cm radius centered on the charge.
(a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface?
(b) What is the value of the point charge?
If the electric field is given by 6i+3j+4k calculate the electric flux through a surface of area 20 units lying in y-z plane.
A uniform line charge with linear density λ lies along the y-axis. What flux crosses a spherical surface centred at the origin with r = R?
Which of the following correctly states Gauss law?
At what point is the electric field intensity due to a uniformly charged spherical shell is maximum?
A charge q is placed at the centre of the open end of cylindrical vessel whose height is equal to its radius. The electric flux of electric field of charge q through the surface of the vessel is
The charge enclosed by a spherical Gaussian surface is 8.85 X 10-8 C. What will be the electric flux through the Surface?
If the electric field is given by 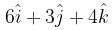 calculate the electric flux through as surface of area 10 units lying in y-z plane.
calculate the electric flux through as surface of area 10 units lying in y-z plane.
The flux associated with a spherical surface is 104 N m2C-1. What will be the flux, if the radius of the spherical shell is doubled?
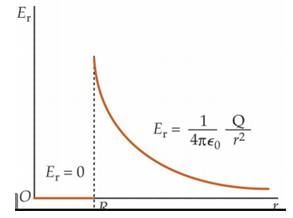
The electric field intensity due to a sphere (solid or hollow) at an external point varies as:



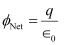
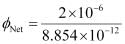

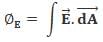
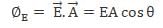
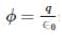 since amount of charge not depends on size and shape so by making radius < double the amount of charge remain same so electric flux remain same.
since amount of charge not depends on size and shape so by making radius < double the amount of charge remain same so electric flux remain same.