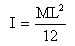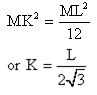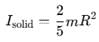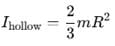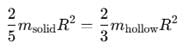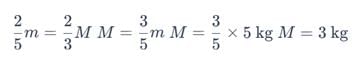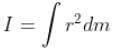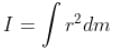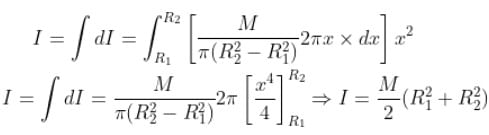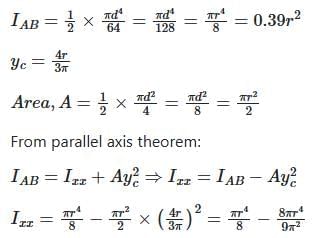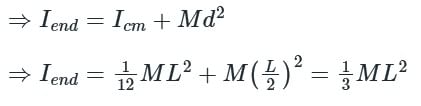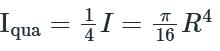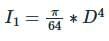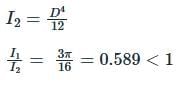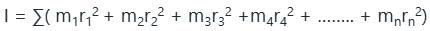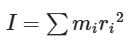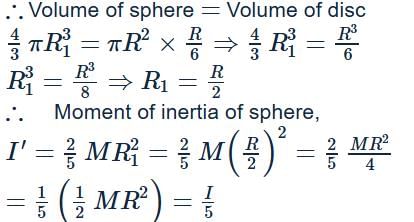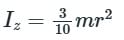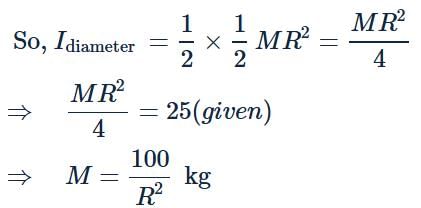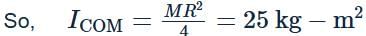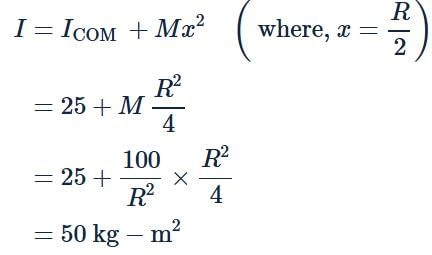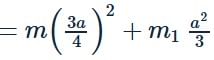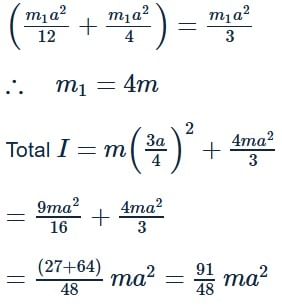Test: Moment of Inertia - JEE MCQ
25 Questions MCQ Test - Test: Moment of Inertia
Two rings have their moment of inertia in the ratio 2:1 and their diameters are in the ratio 2:1. The ratio of their masses will be:
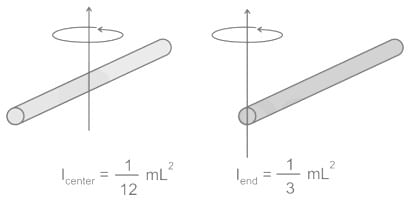
The radius of gyration of uniform rod of length L and mass M about an axis passing through its centre and perpendicular to its length is
Moment of inertia of two spheres of equal radii are equal. One of the spheres is solid and has the mass 5 kg and the other is a hollow sphere. What is the mass of hollow sphere?
There are two circular iron discs A and B having masses in the ratio 1:2 and diameter in the ratio 2:1. The ratio of their moment of inertia is
The moment of inertia of two spheres of equal masses is equal. If one of the spheres is solid of radius  m and the other is a hollow sphere. What is the radius of the hollow sphere?
m and the other is a hollow sphere. What is the radius of the hollow sphere?
The moment of inertia of a solid sphere about its diameter is 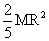 .Find moment of inertia about its tangent.
.Find moment of inertia about its tangent.
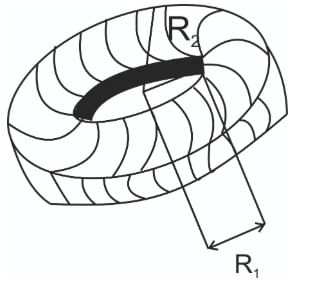
What is the moment of inertia of a disc having inner radius R1 and outer radius R2 about the axis passing through centre and perpendicular to the plane as shown in diagram
A thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be: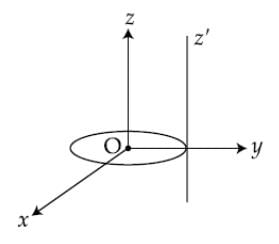
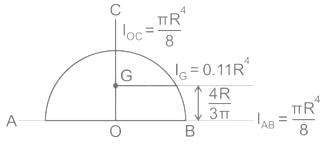
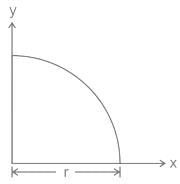
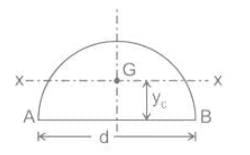
For a semicircular plate of diameter 'D' and radius 'R', with 'y' as the vertical axis passing through the diameter and 'x' as the horizontal axis passing through the diameter, the moment of inertia about the y axis will be:
A thin rod of length L and mass M will have what moment of inertia about an axis passing through one of its ends and perpendicular to the rod?
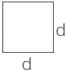
The ratio of moment of inertia of a circular plate to that of a square plate for equal depth is
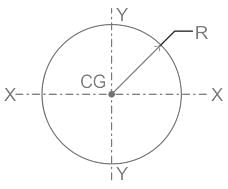
Moment of inertia of a thin spherical shell of mass M and radius R about a diameter is
A circular disc of radius R and thickness R/6 has moment of inertia I about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is :
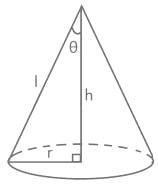
The moment of inertia of a solid cone of mass m and base radius r about its vertical axis is
From a uniform circular disc of radius R and mass 9 M, a small disc of radius R/3 is removed, as shown in the figure. Calculate the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through the centre of the disc.
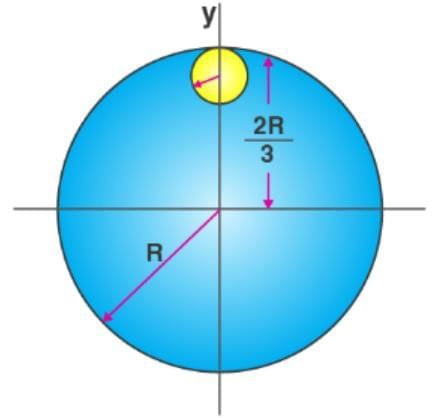
Moment of inertia of a disc of radius R about a diametric axis is 25 kg m2. The moment of inertia of the disc about a parallel axis at a distance R/2 from the centre is
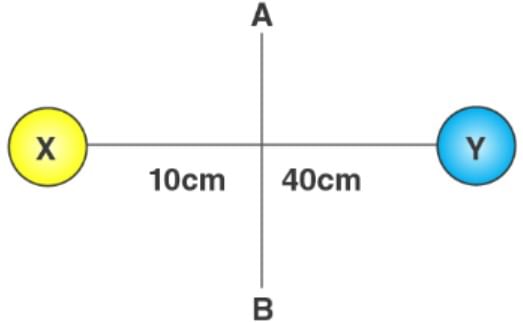
Two balls connected by a rod, as shown in the figure below (Ignore the rod’s mass). The mass of ball X is 700 grams, and the mass of ball Y is 500 grams. What is the moment of inertia of the system about AB? Given: The rotation axis is AB, mX = 700 grams = 0.7 kg, mY = 500 grams = 0.5 kg, rX = 10cm = 0.1m & rY = 40cm = 0.4m.
Moment of inertia of a hollow cylinder of mass M and radius r about its own axis is
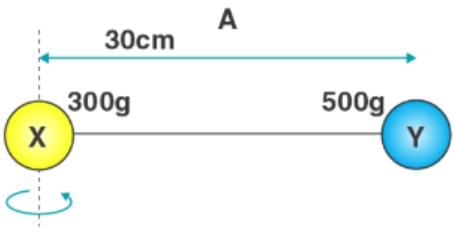
Two balls are connected by a rod, as shown in the figure below (Ignore the rod’s mass). What is the moment of inertia of the system? Given: mX = 300 grams = 0.3 kg, mY = 500 grams = 0.5 kg, rX = 0cm = 0m & rY = 30cm = 0.3m.
Which of the following has the highest moment of inertia when each of them has the same mass and the same outer radius
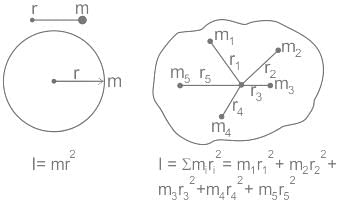
The mass of each ball is 200 grams, and connected by a cord. The length of the cord is 80 cm, and the width of the cord is 40 cm. What is the moment of inertia of the balls about the axis of rotation (Ignore cord’s mass)?
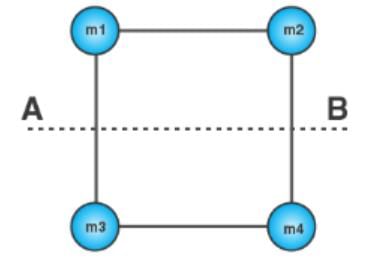
Given
Mass of ball = m1 = m2 = m3 = m4 = 200 gram = 0.2 kg
Distance between the ball and the axis of rotation (r1) = 40cm = 0.4 m
Distance between ball 2 and the axis of rotation (r2) = 40 cm = 0.4 m
Distance between ball 3 and the axis of rotation (r2) = 40 cm = 0.4 m
Distance between ball 4 and the axis of rotation (r2) = 40 cm = 0.4 m
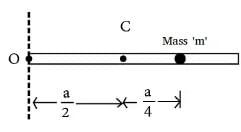
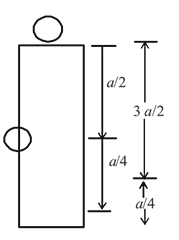
A particle of mass m is attached to a thin uniform rod of length a and mass 4m. The distance of the particle from the centre of mass of the rod is a/4. The moment of inertia of the combination about an axis passing through O normal to the rod is