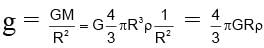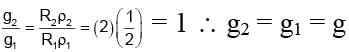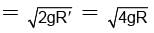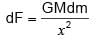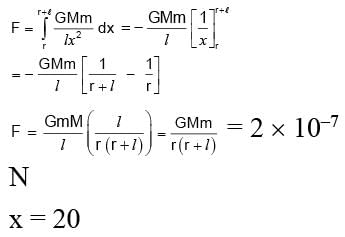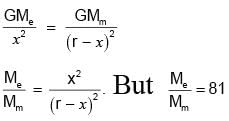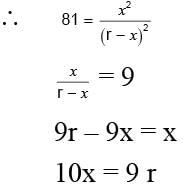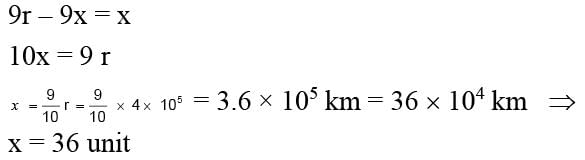Test: Universal Law of Gravitation - JEE MCQ
25 Questions MCQ Test - Test: Universal Law of Gravitation
The gravitational force between two objects each of mass m, separated by a distance r, is F. Gravitational force between two objects each of mass 2m separated by a distance 2r, will be
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. What is the ratio of F:F'?
The earth attracts the moon with a gravitational force of 1020 N. Then the moon attracts the earth with the gravitational force of
What is the force required to produce an acceleration of 9.8 m/s2 on a body of weight 9.8N? Take g = 9.8 m/s2.
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is
Two isolated point masses m and M are separated by a distance l. The moment of inertia of the system about an axis passing through a point where gravitational field is zero and perpendicular to the line joining the two masses, is
The earth attracts the moon with a gravitational force of 1020 N. Then the moon attracts the earth with the gravitational force of
The planet mercury is revolving in an elliptical orbit around Sun as shown.
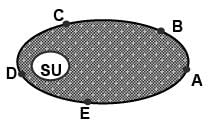
The kinetic energy of mercury will be greatest at
Both earth and moon are subject to the gravitational force of the sun. As observed from the sun, the orbit of the moon
The earth revolves round the sun in an elliptical orbit. Its speed is
Two massive particles of masses M & m (M > m) are separated by a distance l. They rotate with equal angular velocity under their gravitational attraction. The linear speed of the particle of mass m is
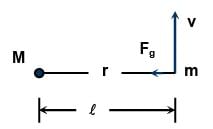
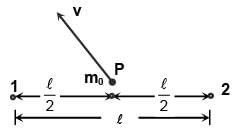
A particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
The gravitational force on a body of mass m at a distance r from the centre of the Earth for r < R, where R is the radius of Earth, is proportional to:
Given below are two statements:
Statement-I: The law of gravitation holds good for any pair of bodies in the universe.
Statement-II: The weight of any person becomes zero when the person is at the center of the earth.
In the light of the above statements, choose the correct answer from the options given below:
A planet has twice the density of earth but the acceleration due to gravity on its surface is exactly the same as on the surface of earth. Its radius in terms of radius of earth R will be
A particle hanging from a spring stretches it by 1 cm at earth’s surface. Radius of earth is 6400 km. At a place 800 km above the earth’s surface, the same particle will stretch the spring by:
A projectile is launched from the surface of the earth with a very high speed v at an angle θ with vertical. What is its velocity when it is at the farthest distance from the earth surface? Given that the maximum height reached by the projectile is equal to the height reached when it is launched perpendicular to earth with a velocity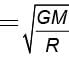 .
.
The mean radius of the earth is R, its angular speed about its own axis is ω and the acceleration due to gravity at the earth surface is g. The cube of radius of orbit of ‘geostationary satellite’ will be:
Two particles of masses M and m are initially at rest and infinitely separated. When they move towards each other due to gravitational attraction, their relative velocity at any instant in terms of distance ‘d’ between them at that instant is
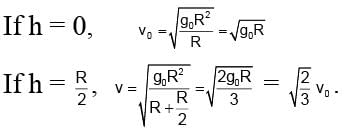
The orbital velocity of an artificial satellite in a circular orbit just above earth’s surface is v0. For a satellite orbiting in a circular orbit at an altitude of half of earth’s radius is
If the radius and density of a planet are two times and half respectively of those of earth, find the intensity of gravitational field at planet surface and escape velocity from planet.
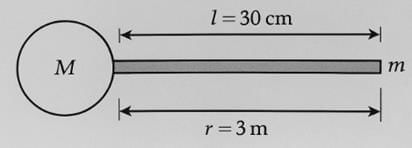
A uniform sphere of mass M = 100 kg and a thin uniform rod of length l = 30cm and mass m = 300 kg oriented as shown in the figure. The distance of centre of sphere to the nearest end of the rod is r = 3 m. The gravitation force between them is given as x
× 10–8 N. Find x
(G = 6.6 × 10–11 Nm2/kg2)
The distance between earth and moon is 4 × 105 km and the mass of earth is 81 times the mass of moon. Find the position (take 104 km as unit) of a point on the line joining the centres of earth and moon, where the gravitational field is zero.
A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m/s as it reaches A. The work done by the person on the mass is –3J. The potential at infinity is –10 J. Then find the potential at A.
Which of the following is the evidence to show that there must be a force acting on earth and directed towards the sun?



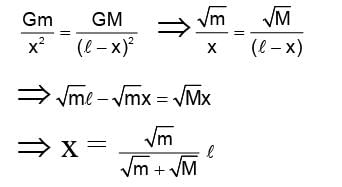
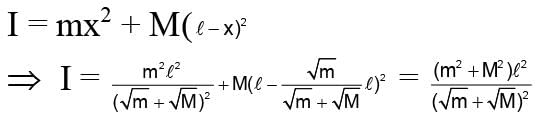
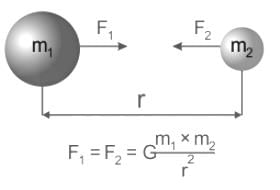
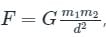 where, F is the gravitational force between bodies, m1, and m2 are the masses of the bodies, d is the distance between the centers of two bodies, and G is the universal gravitational constant.
where, F is the gravitational force between bodies, m1, and m2 are the masses of the bodies, d is the distance between the centers of two bodies, and G is the universal gravitational constant.

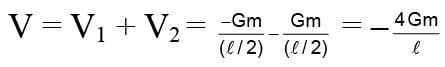
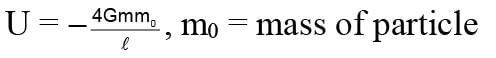
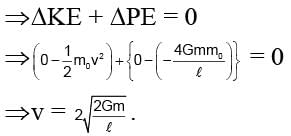
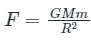
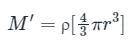
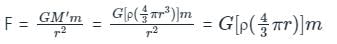
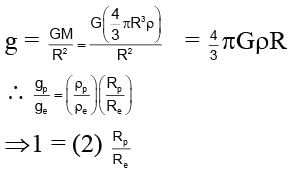
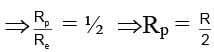
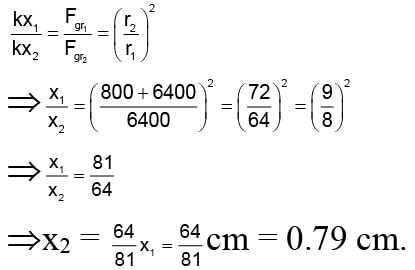
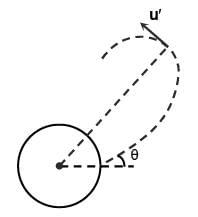

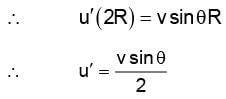
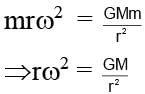
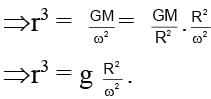
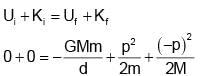
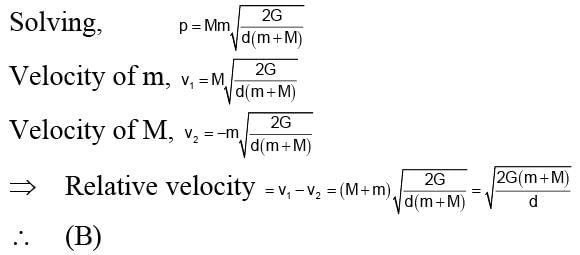
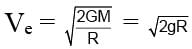
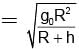 where R is radius of earth.
where R is radius of earth.