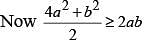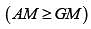Test: Ellipse (21 July) - JEE MCQ
15 Questions MCQ Test - Test: Ellipse (21 July)
The length of the semi-latus-rectum of an ellipse is one third of its major axis, its eccentricity would be
In the ellipse x2 + 3y2 = 9 the distance between the foci is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The eccentric angle of the point where the line, 5x - 3y = 8√2 is a normal to the ellipse +
= 1 is
PQ is a double ordinate of the ellipse x2+ 9y2 = 9, the normal at P meets the diameter through Q at R, then the locus of the mid point of PR is
If F1 & F2 are the feet of the perpendiculars from the foci S1 & S2 of an ellipse +
= 1 on the tangent at any point P on the ellipse, then (S1F1) . (S2F2) is equal to
If tan q1. tan q2 = – then the chord joining two points q1 & q2 on the ellipse
+
= 1 will subtend a right angle at
An ellipse having foci at (3,3) and (-4,4) and passing though the origin has eccentricity equal to
The length of the major axis of the ellipse (5x - 10)2 + (5y + 15)2 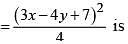
The eccentric angle of a point on the ellipse at a distance of 5/4 units from the focus on the positive x-axis, is
From any point P lying in first quadrant on the ellipse PN is drawn perpendicular to the major axis and produced at Q so that NQ equals to PS, where S is a focus. Then the locus of Q is
If a tangent of slope 2 of the ellipse is normal to the circle x2 + y2 + 4x + 1 = 0 , then the maximum value of ab is


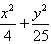 = 1, the length of the major axis is
= 1, the length of the major axis is
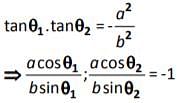
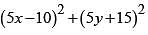
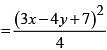
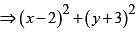
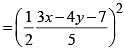
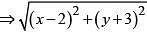
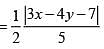
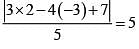
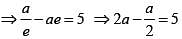
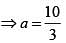
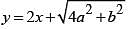 be the tangent
be the tangent