Test: Conic Sections (23 July) - JEE MCQ
15 Questions MCQ Test - Test: Conic Sections (23 July)
The length of the minor axis (along y-axis) of an ellipse in the standard form is 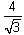 . If this ellipse touches the line x + 6y = 8; then its eccentricity is
. If this ellipse touches the line x + 6y = 8; then its eccentricity is
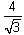 . If this ellipse touches the line x + 6y = 8; then its eccentricity is
. If this ellipse touches the line x + 6y = 8; then its eccentricity isThe locus of mid-points of the line segments joining (-3, -5) and the points on the ellipse  is:
is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The locus of the mid-point of the line segment joining the point (4, 3) and the points on the ellipse x2 + 2y2 = 4 is an ellipse with eccentricity:
Let the eccentricity of an ellipse = 1, a > b, be
. If this ellipse passes through the point
, then a2 + b2 is equal to:
If 3x + 4y = 12is a tangent to the ellipse
= 1 for some a
R, then the distance between the foci of the ellipse is
Which of the following points lies on the locus of the foot of perpendicular drawn upon any tangent to the ellipse, from any of its foci?
Let the eccentricity of the hyperbola be
. If the equation of the normal at the point
on the hyperbola is
x +
y =
, then
is equal to _____. (in integer)
Let the common tangents to the curves 4(x2 + y2) = 9 and y2 = 4x intersect at the point Q. Let an ellipse, centered at the origin O, have lengths of semi-minor and semi-major axes equal to OQ and 6, respectively. If e and l respectively denote the eccentricity and the length of the latus rectum of this ellipse, then 1/e2 is equal to ________. (in integer)
If the ellipse  = 1 meets the line
= 1 meets the line  = 1 on the x-axis and the line
= 1 on the x-axis and the line  = 1 on the y-axis, then the eccentricity of the ellipse is
= 1 on the y-axis, then the eccentricity of the ellipse is
Let the foci of the ellipse = 1 and the hyperbola
coincide. Then the length of the latus rectum of the hyperbola is:
The locus of the midpoints of the chord of the circle x2 + y2 = 25 which is tangent to the hyperbola = 1 is:
Let a line L1 be tangent to the hyperbola = 1 and let L2 be the line passing through the origin and perpendicular to L1. If the locus of the point of intersection of L1 and L2 is (x2 + y2)2 = αx2 + βy2, then α + β is equal to _____.
Let P(3, 3) be a point on the hyperbola, = 1. If the normal to it at P intersects the x-axis at (9, 0) and e is its eccentricity, then the ordered pair (a2, e2) is equal to:
The point P (-2 ,
) lies on the hyerpbola
= 1 having eccentricity
. If the tangent and normal at P to the hyerpbola intersect its conjugate axis at the points Q and R respectively, then QR is equal to:
If the line x - 1 = 0 is a directrix of the hyperbola kx2 - y2 = 6, then the hyperbola passes through the point



 = 1 is:
= 1 is:
 , where m =
, where m = 


 , is (2cos
, is (2cos , 3sin
, 3sin )
)
 ; k =
; k = 
 = 1
= 1 36x2 + 16y2 + 108x + 80y + 145 = 0
36x2 + 16y2 + 108x + 80y + 145 = 0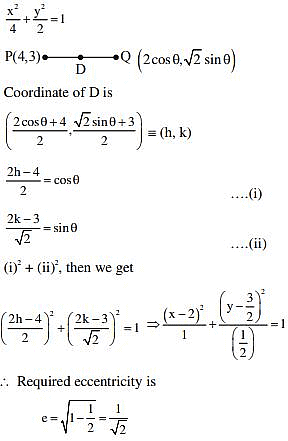


 = 1, if c2 = a2m2 + b2.
= 1, if c2 = a2m2 + b2.
 y = -
y = - x +
x + 
 (3
(3 )2 = a2
)2 = a2 + 9
+ 9 a2 = 9 ×
a2 = 9 ×  = 16
= 16 Eccentricity of ellipse, e =
Eccentricity of ellipse, e = 
 Distance between the foci = 2ae = 2 × 4 ×
Distance between the foci = 2ae = 2 × 4 × 
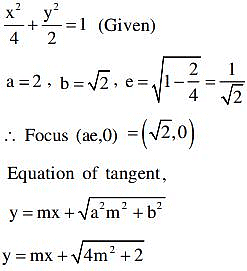
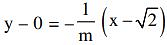
 ) lies on the locus.
) lies on the locus.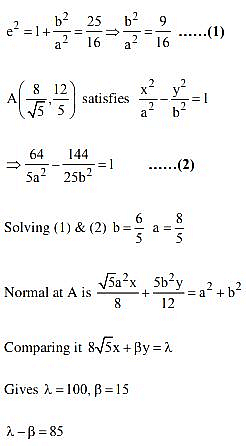


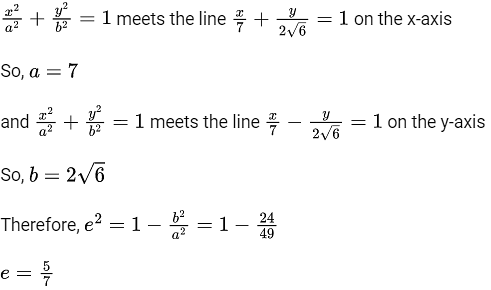


 (x - h)
(x - h)


 ...(i)
...(i) ...(ii)
...(ii) ...(iii)
...(iii) ...(iv)
...(iv) and tanθ =
and tanθ = 
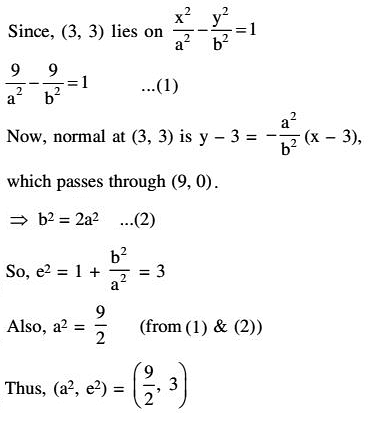

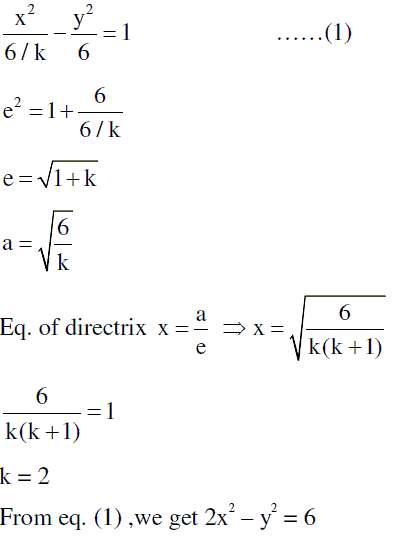
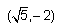 satisfies the above equation.
satisfies the above equation.














