Test: Continuity & Differentiability(3 Sep) - JEE MCQ
15 Questions MCQ Test - Test: Continuity & Differentiability(3 Sep)
Let f : [0,  )
)  [0, 3] be a function defined by:
[0, 3] be a function defined by:
f(x) = 
Then which of the following is true?
f(x) =
Then which of the following is true?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If 'R' is the least value of 'a' such that the function f(x) = x2 + ax + 1 is increasing on [1, 2] and 'S' is the greatest value of 'a' such that the function f(x) = x2 + ax + 1 is decreasing on [1, 2], then the value of |R - S| is _______. (in integer)
Let f : R R and g : R
R be defined as
and
where a, b are non-negative real numbers. If (gof)(x) is continuous for all x R, then a + b is equal to ___________. (in integer)
Let f : R R be defined as f(x) = x3 + x - 5. If g (x) is a function such that f(g(x)) = x,
x ∈ R, then g'(63) is equal to ________.
Let f(x) = min {1, 1 + x sin x}, 0 ≤ x ≤ 2π. If m is the number of points, where f is not differentiable and n is the number of points, where f is not continuous, then the ordered pair (m, n) is equal to
If c is a point at which Rolle's theorem holds for the function f(x) = loge in the interval [3, 4], where
∈ R, then f''(c) is equal to
Let the functions f : and g :
be defined as:
and g(x) =
Then the number of points in where (fog)(x) is NOT differentiable is equal to:
If f(x) = sin and its first derivative with respect to x is -
loge2 when x = 1, where a and b are integers, then the minimum value of |a2 - b2| is ________. (in integer)
Let f, g : R R be two real valued functions defined as f(x) =
and g(x) =
, where k1 and k2 are real constants. If (gof) is differentiable at x = 0, then (gof) (–4) + (gof) (4) is equal to:
The value of loge2(logcosx cosecx) at x =
is
Let R be such that the function f(x) =
is continuous at x = 0, where {x} = x - [x], [x] is the greatest integer less than or equal to x.
Then,
If the function is continuous at x = 0, then k is equal to:
If for p ≠ q ≠ 0, the function f(x) = is continuous at x = 0, then:
The number of points where the function
where [t] denotes the greatest integer ≤ t, is discontinuous is ______________. (in integer)


 t
t  x} in x
x} in x  [0,
[0,  ]
]
 [
[ ,
,  )
)


 ).
). and cot
and cot in sin
in sin and cos
and cos :
: =
= 





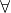 x
x 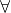 x ∈ [1, 2]
x ∈ [1, 2]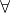 x ∈ [1, 2]
x ∈ [1, 2]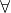 x ∈ [1, 2]
x ∈ [1, 2]



 a + b = 1
a + b = 1 f'(x) = 3x2 + 1
f'(x) = 3x2 + 1  increasing function
increasing function g(x) is the inverse of f(x).
g(x) is the inverse of f(x). g(f(x)) = x
g(f(x)) = x g'(f(x)) f'(x) = 1
g'(f(x)) f'(x) = 1 x3 + x - 5 = 63
x3 + x - 5 = 63 x = 4
x = 4

 f(x) = 1 =
f(x) = 1 =  f(x)
f(x)


 36 + 4
36 + 4 = 48 + 3
= 48 + 3

 = 12
= 12 f'(x) =
f'(x) = 

 2c2 = c2 + 12
2c2 = c2 + 12  c2 = 12
c2 = 12


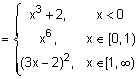

 fog(x) is differentiable for x
fog(x) is differentiable for x  - {0}.
- {0}.
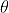
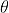 =
= 

 f'(x) =
f'(x) = 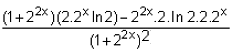
 f'(1) =
f'(1) = 
 |a2 - b2| = 252 - 122
|a2 - b2| = 252 - 122






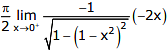
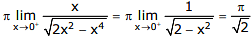



 RHL
RHL  LHL
LHL No value of
No value of  exists.
exists.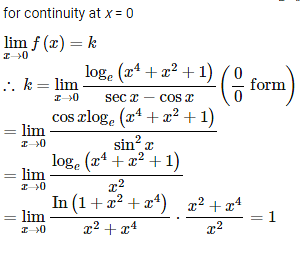


 x =
x = 
 ,
,  and
and 















