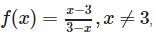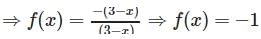AWES TGT Maths Mock Test - 3 - AWES TGT/PGT MCQ
30 Questions MCQ Test - AWES TGT Maths Mock Test - 3
Uttaramerur inscription, which was seen in the news, is found in which state?
Which institution partnered with Starburst to boost India's Aerospace, New Space, and Defence (ASD) startup ecosystem?
What is the name of the bi-annual exercise conducted by the Indian Navy off the Mumbai coast?
Who has been appointed to lead Microsoft's Windows and Surface teams?
In order to help a mentally challenged child in your class, which of the following strategies would you adopt?
Which of the following statements is NOT correct in the context of teaching area- measurement of plane figures?
Learning disabilities can interfere with learning basic skills such as reading, writing and/or math. These can arise due to all listed reasons except:
As a teacher, you firmly believe that informal education has a lot to do in the development of the career of the students. You ask your students to communicate with people, share experiences and gather knowledge from all sources. According to you, informal education refers to
If f : [2, ∞) → B defined by f (x) = x2 - 4x + 5is a bijection, then B =
Let R = {(3, 3), (6, 6), (9, 9), (3,6), (3, 9), (9, 12), (3,12), (6, 12), (12, 12)}, be a relation on the set A = {3, 6, 9, 12} Then the relation is
The coordinates of two diagonally opposite vertices of a rectangle are (4, 3) and (-4,-3). Find the number of such rectangle(s), if the other two vertices also have integral coordinates.
(2015)
Find the values of x and y so that the vectors are equal
Equation of chord AB of circle x2 + y2 = 2 passing through P(2, 2) such that PB/PA = 3, is given by
The equation of the line passing through the centre and bisecting the chord 7x +y -1 = 0 of the ellipse
Tangents are drawn from the points on the line x – y + 3 = 0 to parabola y2 = 8x. Then the variable chords of contact pass through a fixed point whose coordinates are
A team of 7 players is to be formed out of 5 under 19 players and 6 senior players. In how many ways, the team can be chosen when at least 4 senior players are included?
The set of all solutions of the inequality < 1/4 contains the set
If three successive terms in the expansion of (1+x)n a have their coefficients in the ratio 6 : 33 : 110, then n is equal to
The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x = π/2 is equal to
What is the sign of the sinA and tanA in third quadrant respectively
If z1 + z2 + z3 = 0 and |z1| = |z2| = |z3| = 1, then value of equals



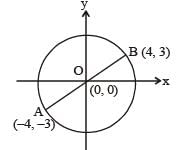

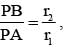 now if r1 = α, r2 = 3α then 4α
now if r1 = α, r2 = 3α then 4α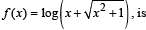
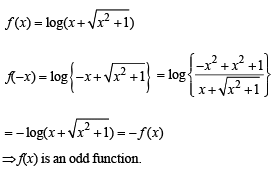
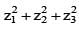
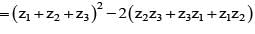
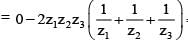
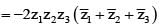
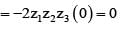
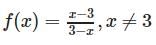 is
is