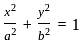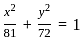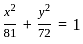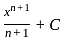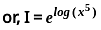UP TGT Mathematics Mock Test - 1 - UPTET MCQ
30 Questions MCQ Test - UP TGT Mathematics Mock Test - 1
Consider the following pairs:
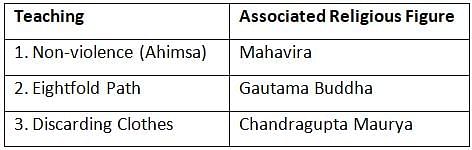
How many of the above pairs are correctly matched?

How many of the above pairs are correctly matched?
Which one of the following statement is incorrect about the beliefs and Faiths of the Kuka Sect:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Who was the Governor of Punjab on behalf of Timur?
Who has been selected as the next CMD of New India Assurance?
if arithmetic mean, geometric mean and harmonic mean between two numbers a and b are A, G & H then A, G H will be
What is the equation of the sphere with unit radius having centre at the origin?
The angle between two vectors -2i + 3j + k and i + 2j – 4k is:
Which among the following is a Skew-symmetric matrix?
What is the solution of the differential equation (x + y) (dx - dy) = dx + dy?
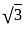 - i ?
- i ?
The value of x for which of the following series converges is
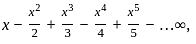
The maximum value of 3 cos θ + 5 sin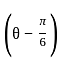 for any real value of θ is
for any real value of θ is
What is the maximum value of the functions 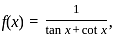 where
where 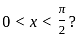
If 1, ω, ω2 are the cube roots of unity, then the value of
(1 + ω2)(1 + ω4)(1 + ω8)(1 + ω16) is
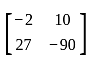 and B = At, where t is transpose of the matrix then a22 of B = ?
and B = At, where t is transpose of the matrix then a22 of B = ?
Find the area of the parabola y2 = 4ax bounded by it's latus rectum.


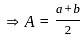
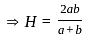
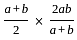
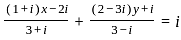
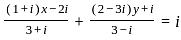
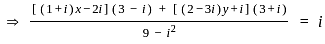
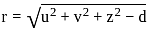
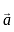 and
and 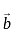 then the dot created is articulated as
then the dot created is articulated as 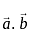
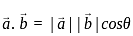
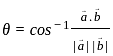
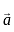 and
and 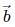



 and
and 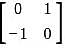 are Skew-symmetric matrix.
are Skew-symmetric matrix.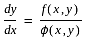 where f(x, y) and ϕ(x, y) are homogeneous functions of the same degree in x and y
where f(x, y) and ϕ(x, y) are homogeneous functions of the same degree in x and y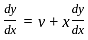
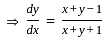
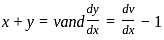
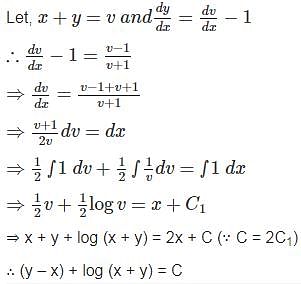
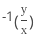
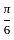
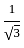
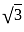
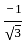
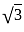
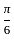
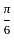
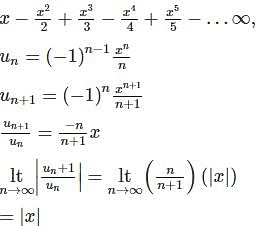
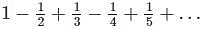
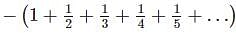
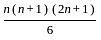
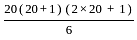
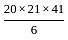
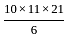
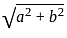
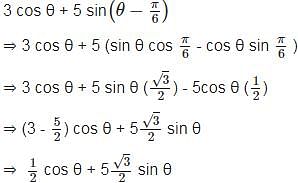
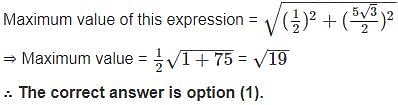
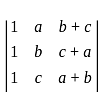
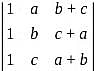
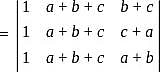
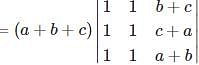
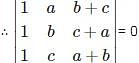
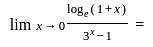
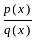 such that,
such that, 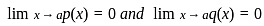 ,
,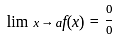 form }
form }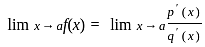
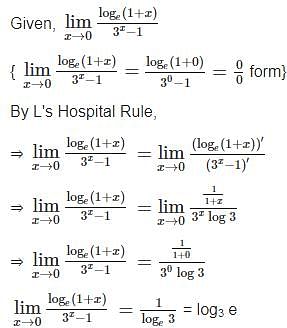
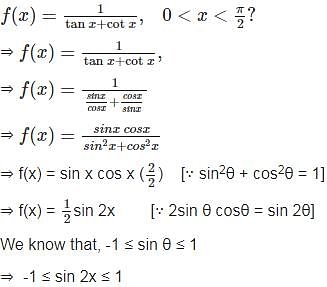
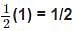
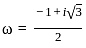
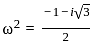
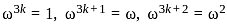
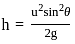
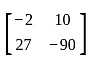
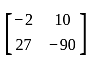
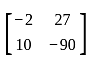
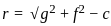
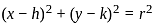
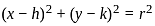
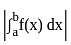 , for curves which are entirely on the same side of the x-axis in the given range.
, for curves which are entirely on the same side of the x-axis in the given range.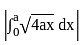
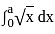
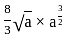 =
= 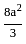 .
.