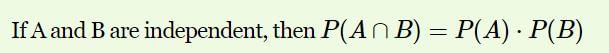Test: Independent Events - Commerce MCQ
10 Questions MCQ Test - Test: Independent Events
A die is tossed twice. The probability of getting 1, 2, 3 or 4 on the first toss and 4, 5, or 6 on the second toss is:
What is the probability of picking a spade from a normal pack of cards and rolling an odd number on a die?
Two parts A and B of a machine is manufactured by a firm. Out of 100 A’s 12 are likely to be defective and Out of 100 B’s 8 are likely to be defective. The probability that a machine manufactured by the firm is free from any defect is:
A and B are two independent events. The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3. The probability of occurrence of A is.
A and B are two independent events. The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3. The probability of occurrence of A is.
Ashmit can solve 80% of the problem given in a book and Amisha can solve 70%. What is the probability that at least one of them will solve a problem selected at random from the book?
If A and B are independent events, such that P(A ∪ B)= 0.7, P(B) = 0.5, then P(A) = ……
A student can solve 70% problems of a book and second student solve 50% problem of same book. Find the probability that at least one of them will solve a selected problem from this book.