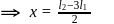Test: Waves and Sound - 2 - JEE MCQ
10 Questions MCQ Test - Test: Waves and Sound - 2
Standing waves are produced by the superposition of two waves
y1 = 0.05 sin(3πt − 2x) and y2 = 0.05 sin(3πt + 2x)
where x and y are expressed in metres and t is in seconds. What is the amplitude of a particle at x = 0.5 m. Given cos(57.3∘) = 0.54
y1 = 0.05 sin(3πt − 2x) and y2 = 0.05 sin(3πt + 2x)
where x and y are expressed in metres and t is in seconds. What is the amplitude of a particle at x = 0.5 m. Given cos(57.3∘) = 0.54
Standing waves are produced by the superposition of two waves
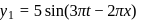
and 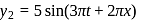
where y and x are in cm and t in second. Find the amplitude of the particle at x = 2 cm.
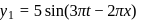
and
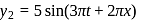
where y and x are in cm and t in second. Find the amplitude of the particle at x = 2 cm.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If  and
and 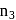 are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequencyn of the string is given by
are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequencyn of the string is given by
An iron load of 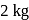 is suspended in air from the free end of a sonometer wire of length
is suspended in air from the free end of a sonometer wire of length  . A tuning fork of frequency
. A tuning fork of frequency 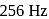 , is in resonance with
, is in resonance with 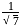 times the length of the sonometer wire. If the load is immensed in water, the length of the wire in metre that will be in resonance with the same tuning fork is (Specific gravity of iron = 8)
times the length of the sonometer wire. If the load is immensed in water, the length of the wire in metre that will be in resonance with the same tuning fork is (Specific gravity of iron = 8)
A sonometer wire of length  is made of steel. The tension in it produces an elastic strain of
is made of steel. The tension in it produces an elastic strain of 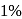 . What is the fundamental frequency of steel if density and elasticity of steel are
. What is the fundamental frequency of steel if density and elasticity of steel are 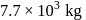 /
/ 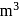 and
and 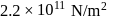 respectively?
respectively?
The frequency of a tuning fork is  and velocity of sound in air is
and velocity of sound in air is 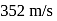 . Find how far the sound has traversed while fork completes 36 vibrations?
. Find how far the sound has traversed while fork completes 36 vibrations?
In a stationary wave represented by y = 2acos(kx)sin(ωt) the intensity at a certain point is maximum when
The vibrations of a string of length 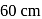 fixed at both the ends are represented by the equation
fixed at both the ends are represented by the equation 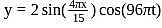 where
where  and
and 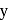 are in
are in 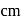 . The maximum number of loops that can be formed in it is
. The maximum number of loops that can be formed in it is
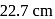 and
and 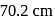 respectively. What will be the end correction?
respectively. What will be the end correction?
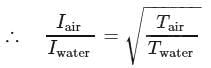
 is placed inside water. The speed of sound in water is
is placed inside water. The speed of sound in water is 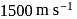 and in the air, it is
and in the air, it is  The frequency of sound recorded by an observer who is standing in the air is
The frequency of sound recorded by an observer who is standing in the air is


 (As string is divided into three segments) But frequency
(As string is divided into three segments) But frequency 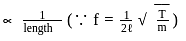
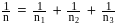
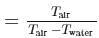
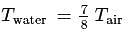
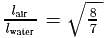
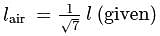
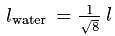
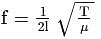
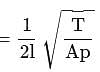
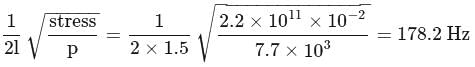
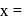 v.t
v.t 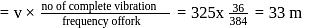
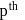 mode of vibration is given by
mode of vibration is given by 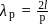
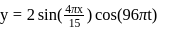

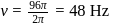 and
and 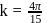
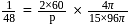
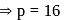
 ,
,