Test: Quadratic Equation - 1 - JEE MCQ
20 Questions MCQ Test - Test: Quadratic Equation - 1
Let α and β are the roots of equation 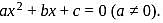 If
If 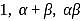 are in arithmetic progression and α, 2, β are in harmonic progression, then the value of
are in arithmetic progression and α, 2, β are in harmonic progression, then the value of 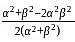 is equal to
is equal to
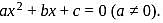 If
If 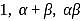 are in arithmetic progression and α, 2, β are in harmonic progression, then the value of
are in arithmetic progression and α, 2, β are in harmonic progression, then the value of 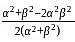 is equal to
is equal to| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If α and β are the roots of the equation 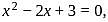 then the sum of roots of the equation having roots as
then the sum of roots of the equation having roots as 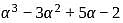 and
and 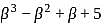 is
is
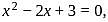 then the sum of roots of the equation having roots as
then the sum of roots of the equation having roots as 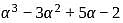 and
and 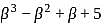 is
isIf α, β are the roots of the equation x2 + bx + c = 0 and α + h,β + h are the roots of the equation x2 + qx + r = 0, then h is equal to
Let x + 1/x = 1 and a, b and c are distinct positive integers such that 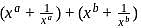
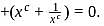 Then the minimum value of (a + b + c) is
Then the minimum value of (a + b + c) is
A value of for which the equations
x2 + bx − 1 = 0
x2 + x + b = 0
have one root in common is
If α, β are real and α2, β2 are the roots of the equation  and β2 ≠ 1, then β2 =
and β2 ≠ 1, then β2 =
If one root of the equation (ℓ−m)x2 + ℓx + 1 = 0 is double the other and ℓ is real, then what is the greatest value of m ?
If α ≠ β but α2 = 5α−3 and β2 = 5β − 3 then the equation having α / β and β / α as its roots is
If a, b, c ∈ R and the equations ax2 + bx + c = 0
a ≠ 0, has real roots α and β satisfying α < −1
and β > 1, then  is
is
If the roots of ax2 + bx + c = 0 are sinα and cos α for some α, then which one of the following is correct?
If λ ≠ μ and λ2 = 5λ − 3, μ2 = 5μ − 3, then the equation whose roots are λ / μ and μ / λ is
If 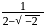 is one of the roots of ax2 +bx + c = 0, where a,b,c are real, then what are the values of a, b, c respectively?
is one of the roots of ax2 +bx + c = 0, where a,b,c are real, then what are the values of a, b, c respectively?
If the roots of the equations px2 + 2qx + r = 0 and qx2 − 2−√prx + q = 0 be real, then
Consider ,such that f(3) > 0 and f(2) ≤ 0. If α and β are the roots of equation f(x) = 0 then the value of α2 + β2 is equal to
If 0 < a < b < c and the roots α, β of the equation ax2 + bx + c = 0 are imaginary then incorrect statement is
If z1,z2 are the roots of the quadratic equation az2 + bz + c = 0 such that Im(z1, z2) ≠ 0 then (Assume that complex roots are not conjugate to each other)
Suppose the quadratic equations x2 + px + q = 0 and x2 + rx + s = 0 are such that p,q,r,s are real and pr = 2(q + s). Then


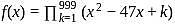 , then product of all real roots of f(x) = 0 is
, then product of all real roots of f(x) = 0 is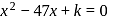
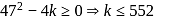

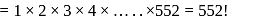
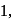
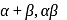 are in A.P.
are in A.P. 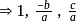 are in A.P.
are in A.P.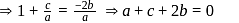 …
… 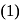
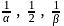 are in A.P.
are in A.P. 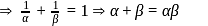
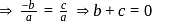 …
… 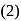
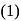 &
&  we get,
we get,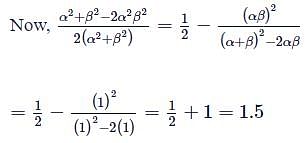

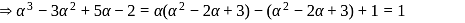
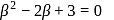
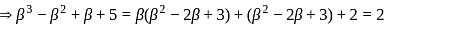
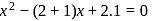
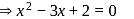
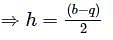
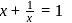
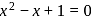
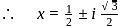
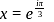
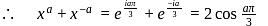
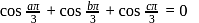

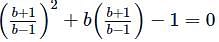
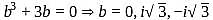
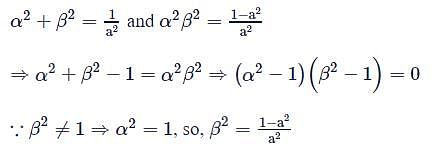
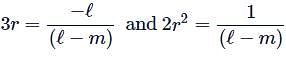
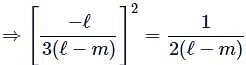
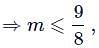 Hence maximum value of m = 9/8
Hence maximum value of m = 9/8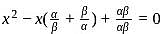
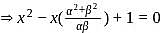
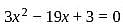
 and
and 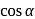 be the roots of
be the roots of 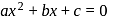
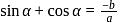 and
and 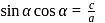
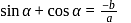
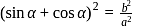
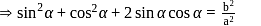

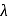 and
and 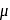 are the roots of
are the roots of 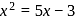 or
or 
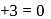
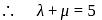 and
and 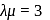
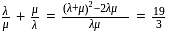
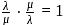
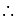 Desired equation is
Desired equation is 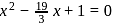
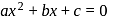 whose one root is
whose one root is 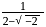
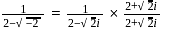

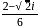 (∴ complex roots always occurs in pairs )
(∴ complex roots always occurs in pairs )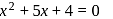 or
or 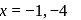 but
but 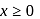
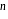 becomes
becomes 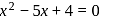 or x = 1, 4 both values are non admissible,
or x = 1, 4 both values are non admissible,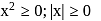
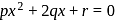 ...(i)
...(i)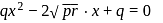 ...(ii)
...(ii) (using discriminant)
(using discriminant) ...(iii)
...(iii)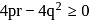
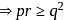 ...(iv)
...(iv)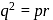 .
.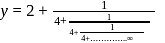 then
then
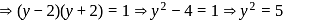
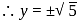 since
since 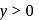
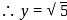
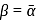
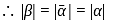
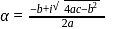
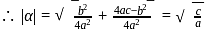
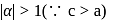
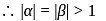
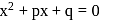 be
be 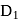 , then
, then 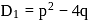 and
and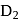 of the equation
of the equation 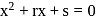 is
is 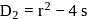
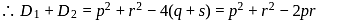 [from the given relation]
[from the given relation]