Test: Packing Efficiency (Old NCERT) - JEE MCQ
10 Questions MCQ Test - Test: Packing Efficiency (Old NCERT)
Packing efficiency of body centred cubic unit cell is:
Packing efficiency in a unit cell is never 100% because constituent particles are assumed to be:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
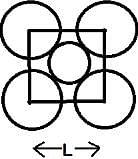
The packing efficiency of the two-dimensional square unit cell shown in the given figure is:

Packing efficiency in a unit cell is never 100% because constituent particles are assumed to be:
What is the dimensional formula of packing fraction?
Arrange the types of arrangement in terms of decreasing packing efficiency.
Which of the following shows maximum packing efficiency?
What are the percentages of free space in a CCP and simple cubic lattice?
If metallic atoms of mass 197 and radius 166 pm are arranged in ABCABC fashion then what is the surface area of each unit cell?
If copper, density = 9.0 g/cm3 and atomic mass 63.5, bears face-centered unit cells then what is the ratio of surface area to volume of each copper atom?







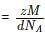
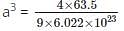
 127.46 pm
127.46 pm














