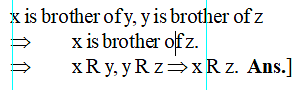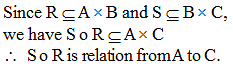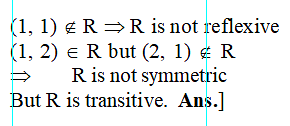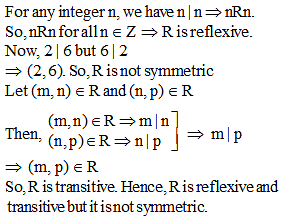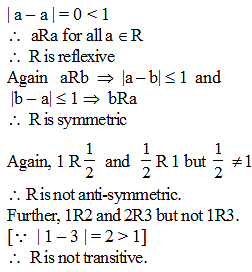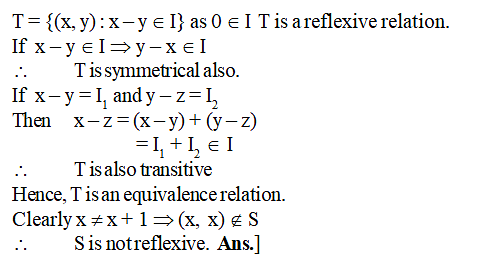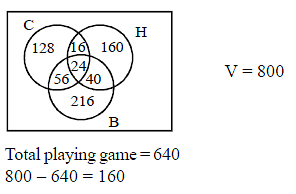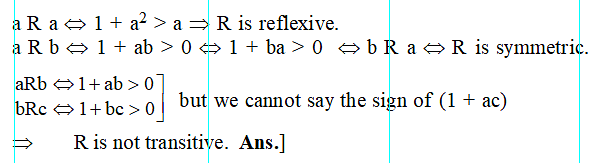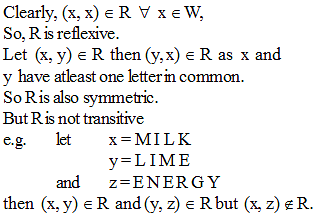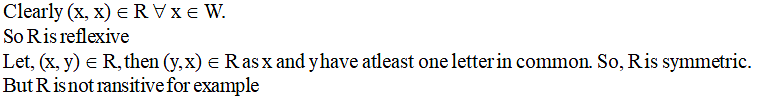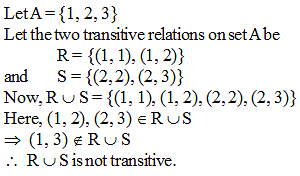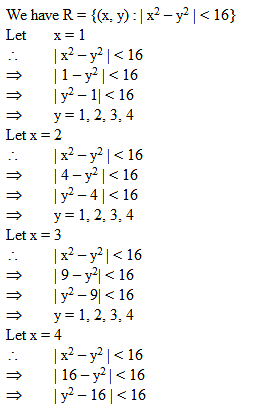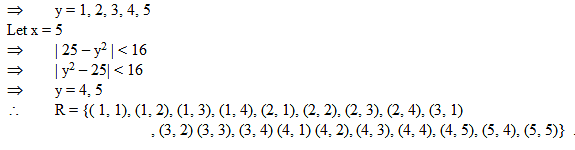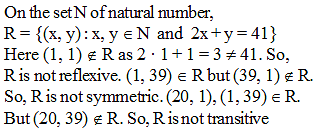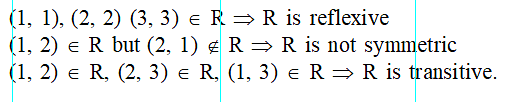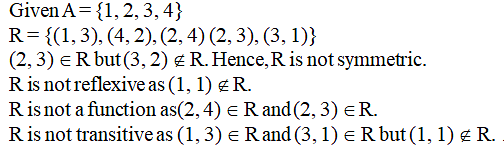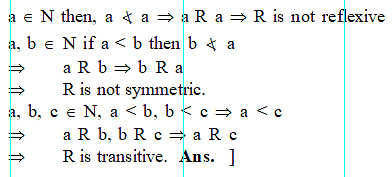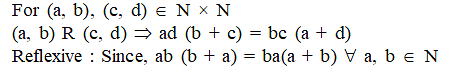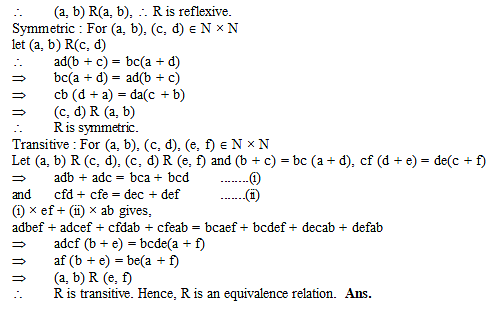Sets, Relations and Functions - 1 - Free MCQ Test with solutions for JEE

The relation R defined in A = {1, 2, 3} by aRb if |a² – b²| ≤ 5. Which of the following is false

Let R : A → A, A is set of all children in a family such that x R ⇒ y  x is brother of ‘y’ (where x, y ∈ A), then R is-

A relation R is defined from {2, 3, 4, 5} to {3, 6, 7, 10} by xRy ⇔ x is relatively prime to y. Then domain of R is

If R is relation from a set A to a set B and S is a relation from B to C, then the relation S o R

Let A = {1, 2, 3, 4}, and let R = {(2, 2), (3, 3), (4, 4), (1, 2)} be a relation on A. Then R is-

If R is a relation from a finite set A having m elements to a finite set B having n elements, then the number of relations from A to B is-

Given the relation R = {(2, 3), (3,4)}  on the set {2, 3, 4}. The number of minimum number of ordered pairs to be added to R so that R is  reflexive and symmetric –

Let P and Q be two equivalence relations on a set A. Then

The void relation on a set  A  is

An integer m is said to be related to another integer n if m is a multiple of n. Then, the relation is

Let R be the relation on the set of all real numbers defined by   aRb  iff  | a – b | ≤ 1. Then, R is

Let R be the real line. Consider the following subsets of the plane R × R :

S = {(x, y): y = x + 1 and 0 < x < 2}

T = {(x, y) : x – y is an integer}.

Which one of the following is true ?

Out of 800 boys in a school, 224 played cricket, 240 played hockey and 336 played basketball of the total , 64 played both basketball and hockey, 80 played cricket and basketball and 40 played cricket and hockey, 24 played all the three games. The number of boys who play only cricket is

Let R {(3, 3), (6, 6), (9, 9), (12, 12) (6, 12) (3, 9) (3, 12), (3, 6)} be a relation on the set  A = {3, 6, 9, 12}. The relation is -

Let R be a relation defined in the set of real numbers by a R b ⇔ 1 + ab > 0. Then R is-

The minimum number of elements that must be added to the relation R = {(1, 2), (2, 3)} on the set {1,2,3}, so that it is equivalence is-

Let  W denote the words in the English dictionary. Define the relation R by

R = {(x,y) ∈ W × W | the words x and y have atleast one letter in common |

Then  R  is

Let R and S be two non-void relations on a set A. Which of the following statements is false?

For real numbers x and y, we write x R y ⇔ x – y + √2 is an irrational number. Then the relation R is -

The relation R defined on the set A = {1, 2, 3, 4, 5} by R = {(x, y) : | x² – y² | < 16} is given  by

Let R be a relation on the set N defined by {(x, y): x, y ∈ N and 2x + y = 41}. Then R is

The relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on the set A = {1, 2, 3} is -

Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a releation on the set A = {1, 2, 3, 4}. The relation R is-

Let A = {2, 3, 4, 5} and let

R = {(2, 2), (3, 3), (4, 4), (5, 5), (2, 3), (3, 2), (3, 5), (5, 3)} be a relation in A. Then R is -

The relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on the set A = {1, 2, 3} is -

The relation "less than" in the set of natural numbers is

Let N denote the set of all natural numbers and R be the relation on N × N defined by  (a, b) R (c, d) if ad (b + c) = bc (a + d), then R is-

Let A be the set of all positive integers, and define a relation R on A by
“a R b if and only if a divides b.”
Which of the following correctly describes R?