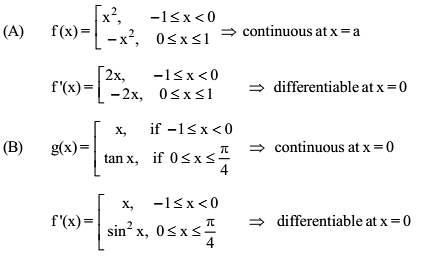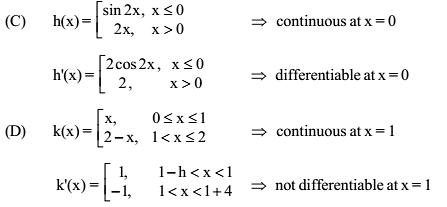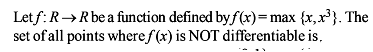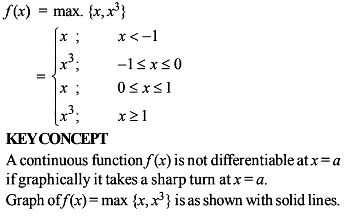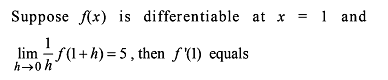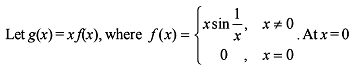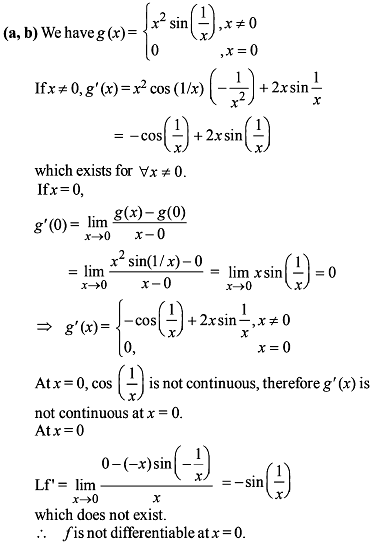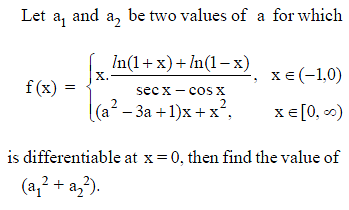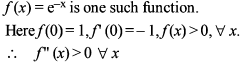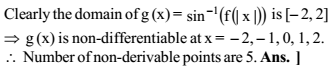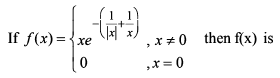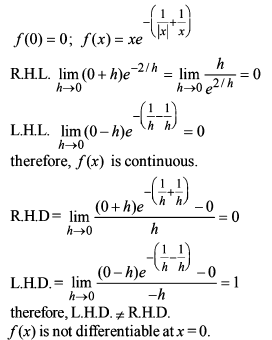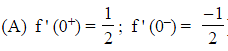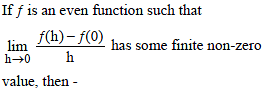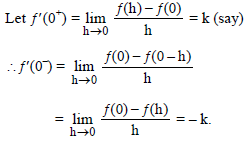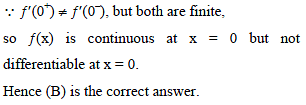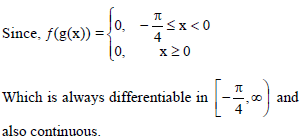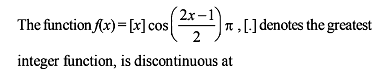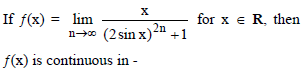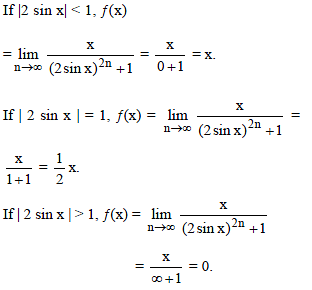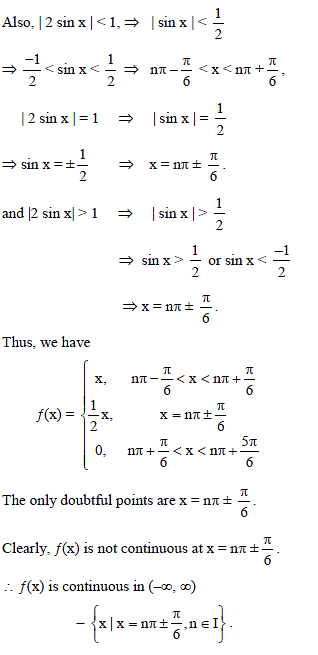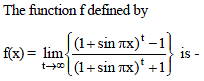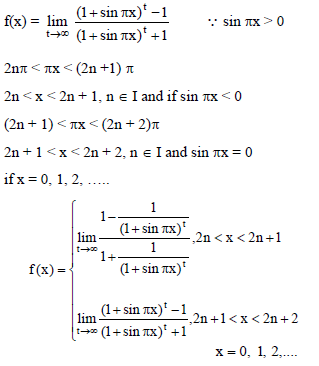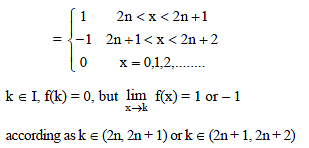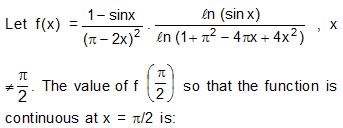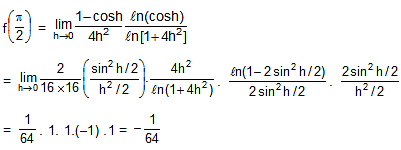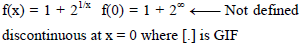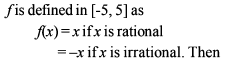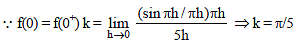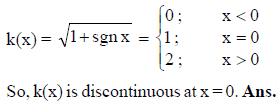Continuity and Differentiability - 1 - JEE MCQ
Test Description
30 Questions MCQ Test - Continuity and Differentiability - 1
Continuity and Differentiability - 1 for JEE 2024 is part of JEE preparation. The Continuity and Differentiability - 1 questions and answers have been prepared
according to the JEE exam syllabus.The Continuity and Differentiability - 1 MCQs are made for JEE 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Continuity and Differentiability - 1 below.
Solutions of Continuity and Differentiability - 1 questions in English are available as part of our course for JEE & Continuity and Differentiability - 1 solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Continuity and Differentiability - 1 | 30 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Continuity and Differentiability - 1 - Question 1
Which one of the following is not true always?
Detailed Solution for Continuity and Differentiability - 1 - Question 1
Continuity and Differentiability - 1 - Question 2
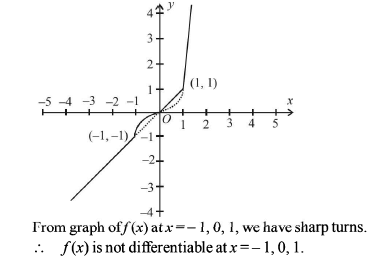
Which of the following functions defined below are NOT differentiable at the indicated point?
Detailed Solution for Continuity and Differentiability - 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for Continuity and Differentiability - 1 - Question 3
Detailed Solution for Continuity and Differentiability - 1 - Question 4
Continuity and Differentiability - 1 - Question 5
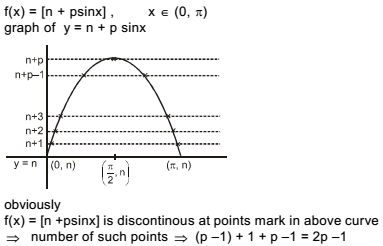
Let f(x) = [n + p sin x], x ∈ (0, π), n ∈ Z, p is a prime number and [x] is greatest integer less than or equal to x. The number of points at which f(x) is not differentiable is
Detailed Solution for Continuity and Differentiability - 1 - Question 5
Detailed Solution for Continuity and Differentiability - 1 - Question 6
Detailed Solution for Continuity and Differentiability - 1 - Question 7
Detailed Solution for Continuity and Differentiability - 1 - Question 8
Detailed Solution for Continuity and Differentiability - 1 - Question 9
Detailed Solution for Continuity and Differentiability - 1 - Question 10
Continuity and Differentiability - 1 - Question 11
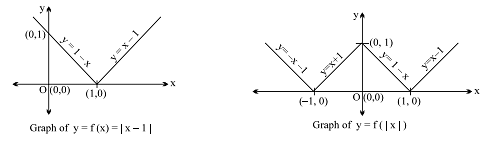
If f (x) = | 1 – x |, then the number of points where g (x) = sin–1(f (| x|)) is non-differentiable, are
Detailed Solution for Continuity and Differentiability - 1 - Question 11
Detailed Solution for Continuity and Differentiability - 1 - Question 12
Continuity and Differentiability - 1 - Question 13
If f: R → R be a differentiable function, such that f(x + 2y) = f(x) + f(2y) + 4xy ∀ x, y ∈ R. then
Detailed Solution for Continuity and Differentiability - 1 - Question 13
Detailed Solution for Continuity and Differentiability - 1 - Question 14
Continuity and Differentiability - 1 - Question 15
Which one of the following function is differentiable at x = 0?
Detailed Solution for Continuity and Differentiability - 1 - Question 15
Detailed Solution for Continuity and Differentiability - 1 - Question 16
Detailed Solution for Continuity and Differentiability - 1 - Question 17
Detailed Solution for Continuity and Differentiability - 1 - Question 18
Continuity and Differentiability - 1 - Question 19
The function ƒ(x) = [x]2 – [x2] (where [y] is the greatest integer less than or equal to y), is discontinuous at -
Detailed Solution for Continuity and Differentiability - 1 - Question 19
Detailed Solution for Continuity and Differentiability - 1 - Question 20
Detailed Solution for Continuity and Differentiability - 1 - Question 21
Detailed Solution for Continuity and Differentiability - 1 - Question 22
Detailed Solution for Continuity and Differentiability - 1 - Question 23
Detailed Solution for Continuity and Differentiability - 1 - Question 24
Detailed Solution for Continuity and Differentiability - 1 - Question 25
Detailed Solution for Continuity and Differentiability - 1 - Question 26
Detailed Solution for Continuity and Differentiability - 1 - Question 27
Detailed Solution for Continuity and Differentiability - 1 - Question 29
Continuity and Differentiability - 1 - Question 30
Which one of the following function is discontinuous for atleast one real value of x?
[Note : sgn x denotes signum function of x.]
Detailed Solution for Continuity and Differentiability - 1 - Question 30
Information about Continuity and Differentiability - 1 Page
In this test you can find the Exam questions for Continuity and Differentiability - 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Continuity and Differentiability - 1, EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for JEE
Important Questions for Continuity and Differentiability - 1
Find all the important questions for Continuity and Differentiability - 1 at EduRev.Get fully prepared for Continuity and Differentiability - 1 with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the Continuity and Differentiability - 1 syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of Continuity and Differentiability - 1 resources.
Continuity and Differentiability - 1 MCQs with Answers
Prepare for the Continuity and Differentiability - 1 within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for Continuity and Differentiability - 1
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace Continuity and Differentiability - 1 with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup