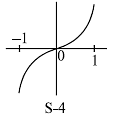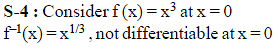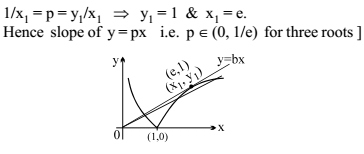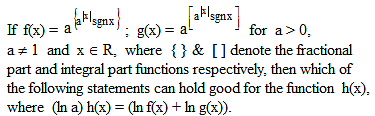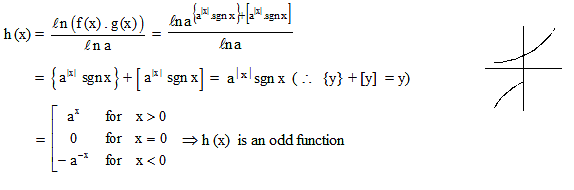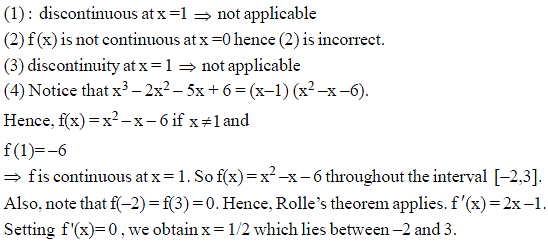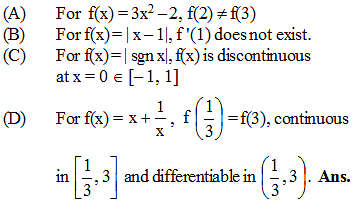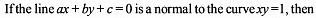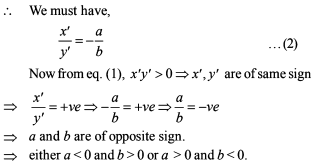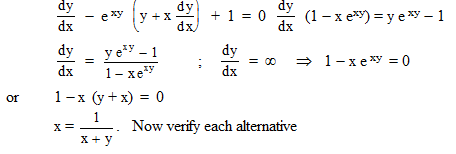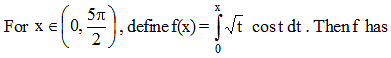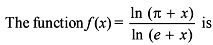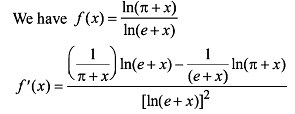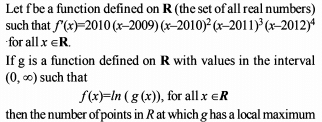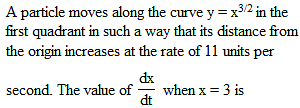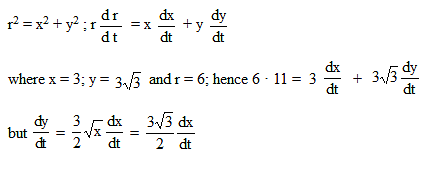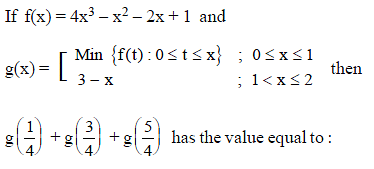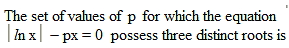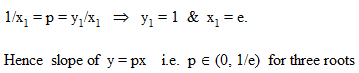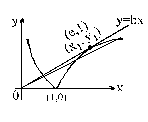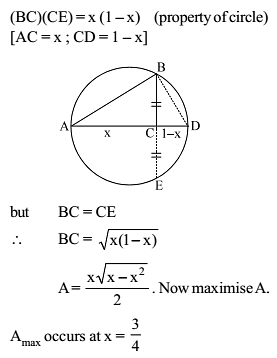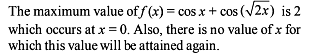Application of Integrals - 2 - JEE MCQ
30 Questions MCQ Test - Application of Integrals - 2
Give the correct order of initials T or F for following statements. Use T if statement is true and F if it is false.
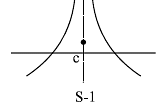
Statement-1: If f : R → R and c ∈ R is such that f is increasing in (c – δ, c) and f is decreasing in (c, c + δ) then f has a local maximum at c. Where δ is a sufficiently small positive quantity.
Statement-2 : Let f : (a, b) → R, c ∈ (a, b). Then f can not have both a local maximum and a point of inflection at x = c.
Statement-3 : The function f (x) = x2 | x | is twice differentiable at x = 0.
Statement-4 : Let f : [c – 1, c + 1] → [a, b] be bijective map such that f is differentiable at c then f–1 is also differentiable at f (c).
The set of values of p for which the equation |ln x|–px = 0 possess three distinct roots is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which one of the following functions Rolle’s theorem is applicable?
For which one of the following function Rolle's theorem is applicable?
The curve y - exy + x = 0 has a vertical tangent at :
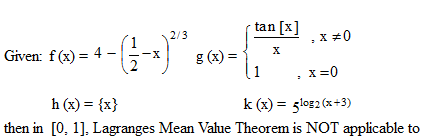
where [x] and {x} denotes the greatest integer and fraction part function.
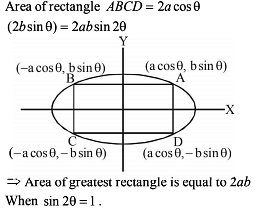
P and Q are two points on a circle of centre C and radius α, the angle PCQ being 2θ then the radius of the circle inscribed in the triangle CPQ is maximum when
Let P be the point on the curve 4x2 + a2y2 = 4a2, 0 < a2 < 8 whose distance from Q(0, – 2) is greatest. If R is the reflection of P in the x-axis then find the least distance of R from the line 3x – 4y + 7 = 0 is
A right triangle is drawn in a semicircle of radius 1/2 with one of its legs along the diameter. The maximum area of the triangle is
Top Courses for JEE
Important Questions for Application of Integrals - 2
Application of Integrals - 2 MCQs with Answers
Online Tests for Application of Integrals - 2
|
© EduRev
|
Education Revolution
|
|
