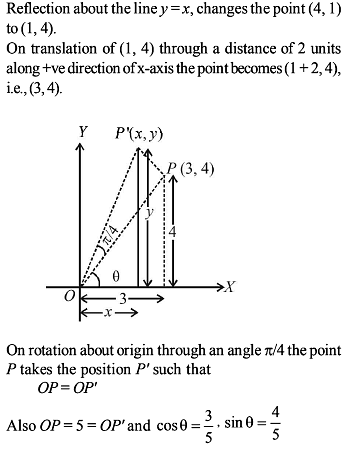
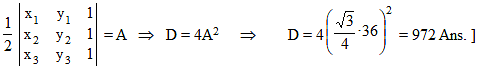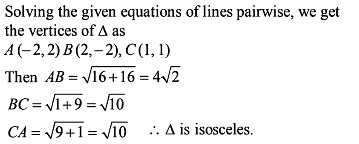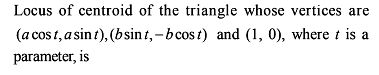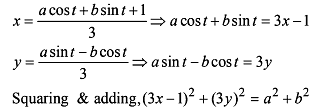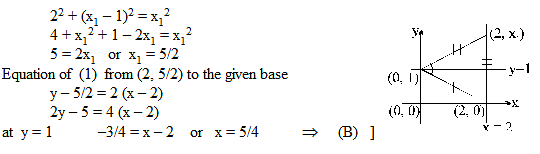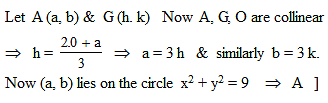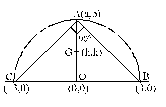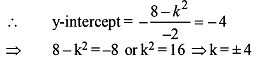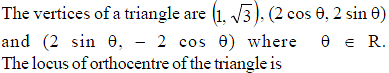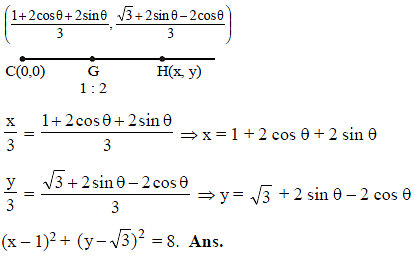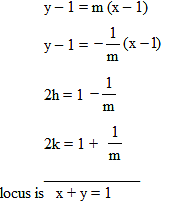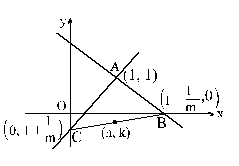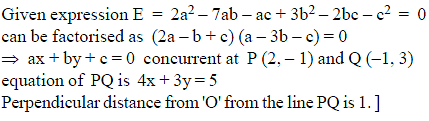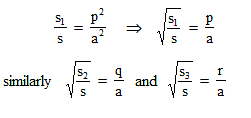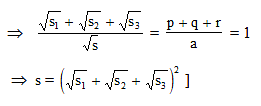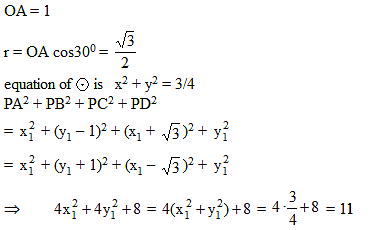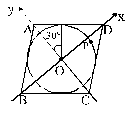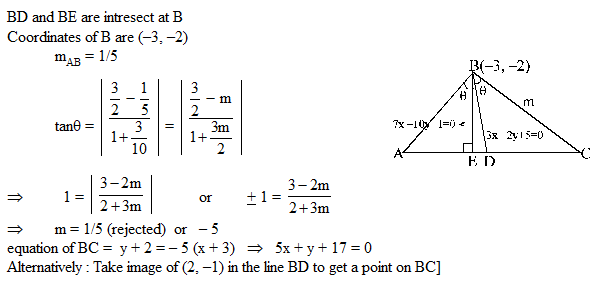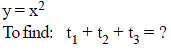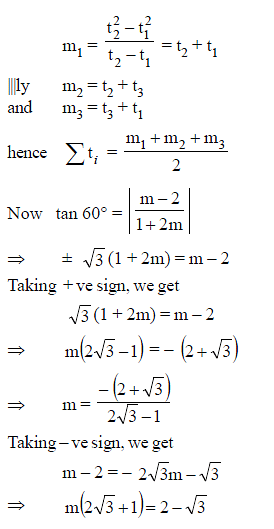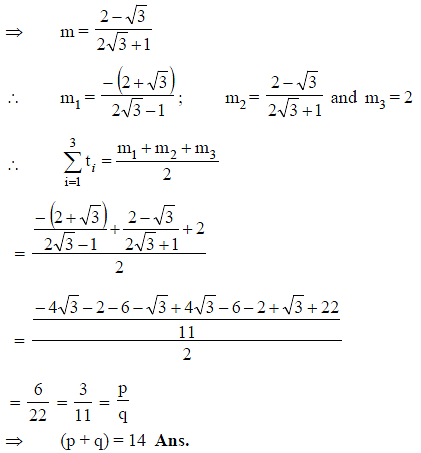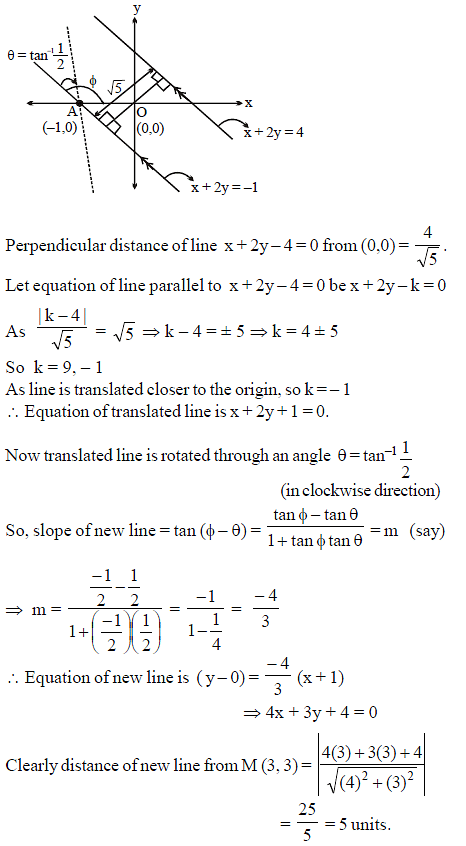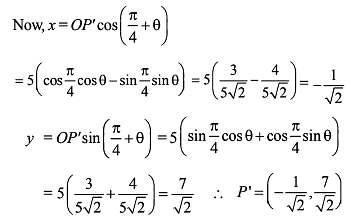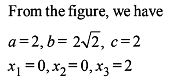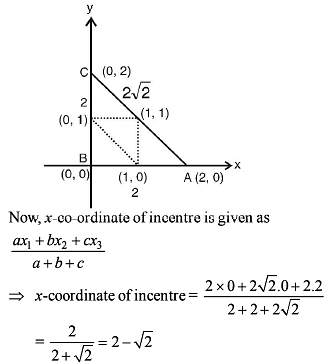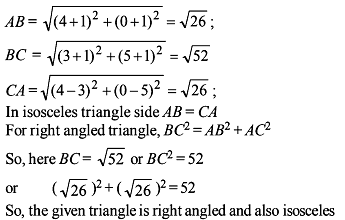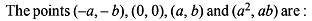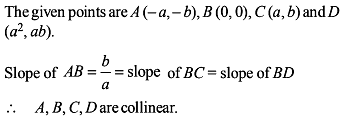Straight Lines - 1 - JEE MCQ
30 Questions MCQ Test - Straight Lines - 1
The point which divides the joint of (1, 2) and (3,4) externally in the ratio 1 : 1.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The line through the points (a , b) and (- a, - b) passes through the point
The equation y−y1 = m (x−x1), m ∈ R, represents all lines through the point (x1,y1) except the line
The straight lines x + y = 0 , 3x + y – 4 = 0 , x + 3y – 4 = 0 form a triangle which is
The vertex A of a triangle ABC is the point (-2, 3) whereas the line perpendicular to the sides AB and AC are x – y – 4 = 0 and 2x – y – 5 = 0 respectively. The right bisectors of sides meet at P(3/2 , 5/2) . Then the equation of the median of side BC is
The ends of the base of an isosceles triangle are at (2, 0) and (0, 1) and the equation of one side is x = 2 then the orthocentre of the triangle is
B & C are fixed points having co-ordinates (3, 0) and (- 3, 0) respectively. If the vertical angle BAC is 90º, then the locus of the centroid of the D ABC has the equation :
Given A(1, 1) and AB is any line through it cutting the x-axis in B. If AC is perpendicular to AB and meets the y-axis in C, then the equation of locus of mid- point P of BC is
If 2a2 – 7ab – ac + 3b2 – 2bc – c2 = 0 then the family of lines ax + by + c = 0 are either concurrent at the point P(x1, y1) or at the point Q(x2, y2). Find the distance of the origin from the line passing through the points P and Q, the distance being measured parallel to the line 3x – 4y = 2.
Three straight lines are drawn through a point P lying in the interior of the D ABC and parallel to its sides. The areas of the three resulting triangles with P as the vertex are s1, s2 and s3. The area of the triangle in terms of s1, s2 and s3 is :
In a triangle ABC , if A (2, – 1) and 7x – 10y + 1 = 0 and 3x – 2y + 5 = 0 are equations of an altitude and an angle bisector respectively drawn from B, then equation of BC is
An equilateral triangle ABC is inscribed in the parabola y = x2 and one of the side of the equilateral triangle has the gradient 2. If the sum of x-coordinates of the vertices of the triangle is a rational in the form p/q where p and q are coprime, then find the value of (p + q).
Line x + 2y = 4 is translated by √5 units closer to the origin and then rotated by angle tan–1 1/2 in the clockwise direction about the point where the shifted line cuts the x-axis. Find the distance of new line from M(3, 3).