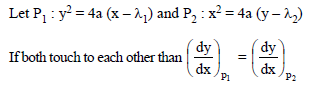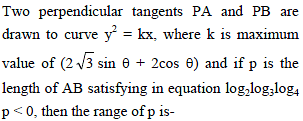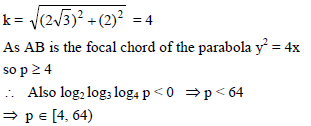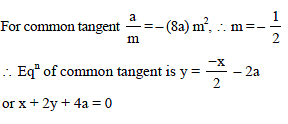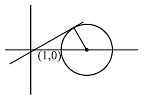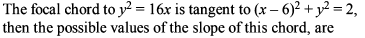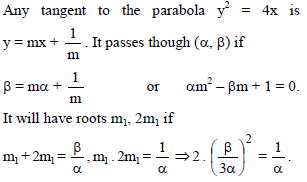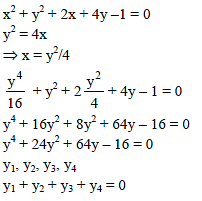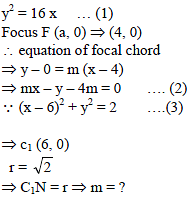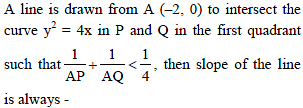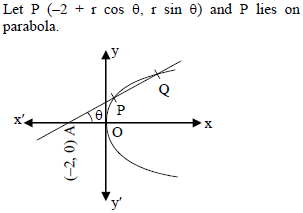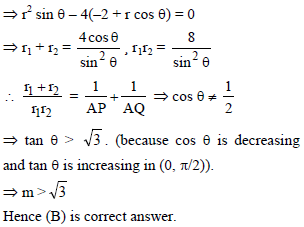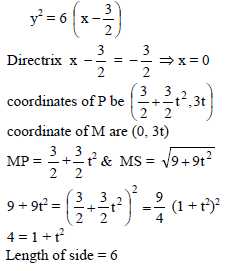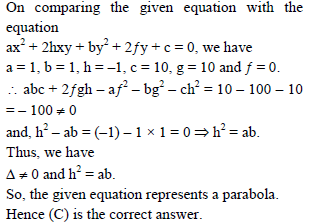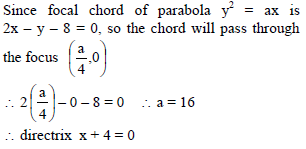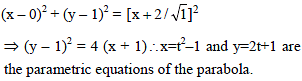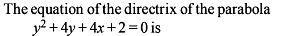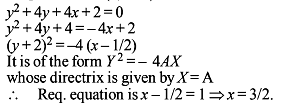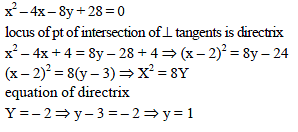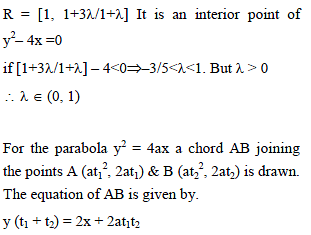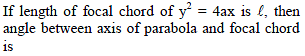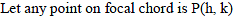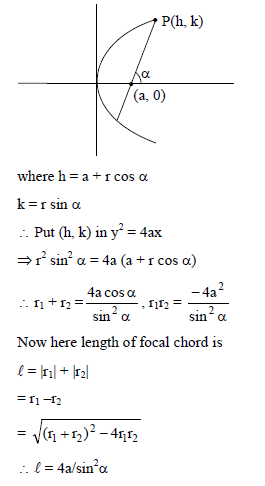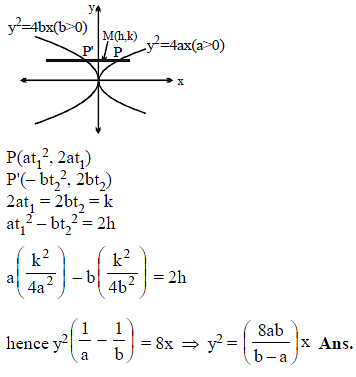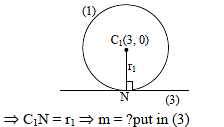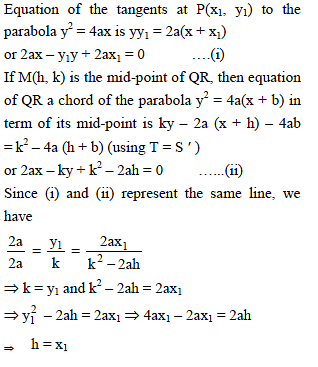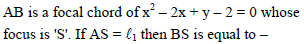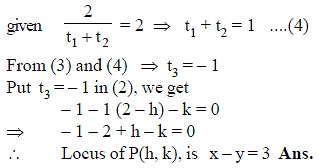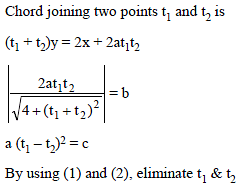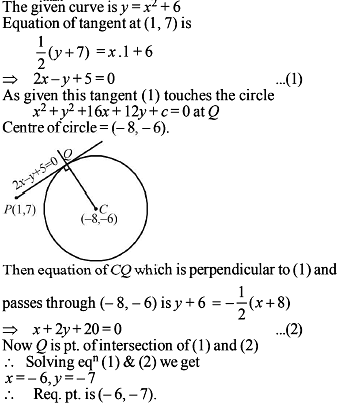Parabola - 1 - JEE MCQ
30 Questions MCQ Test - Parabola - 1
Two parabolas y2 = 4a (x –λ1) and x2 = 4a (y – λ2) always touch each other, λ1 and λ2 being variable parameters. Then, their points of contact lie on a
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The common tangent to the parabolas y2 = 4ax and x2 = 32 ay has the equation –
Write the correct order sequence in respect of the statement given below. F stands for false and T stands for true.
If a variable circle is described to pass through the point (1, 0) and tangent to the curve y = tan (tan–1 x). The locus of the centre of the circle is a parabola whose
I. length of the latus rectum is 2 √2
II. axis of symmetry has the equation x + y = 1
III. vertex has the co-ordinates (3/4, 1/4)
IV. directrix is x – y = 0
If two tangents drawn from the point (α, β) to the parabola y2 = 4x be such that the slope of one tangent is double of the other then -
The normal y = mx – 2am – am2 to the parabola y2 = 4ax subtends a right angle at the origin, then-
The focal chord to y2 = 16x is tangent to (x – 6)2 + y2 = 2, then the possible values of the slope of this chord, are-
If P be a point on the parabola y2 = 3(2x–3) and M is foot of perpendicular drawn from P on the directrix of the parabola, then length of each side of an equilateral triangle SMP, where S is focus of the parabola is
The name of the conic represented by the equation x2 + y2 – 2xy + 20x + 10 = 0 is
If focal chord of the parabola y2 = ax is 2x – y – 8 = 0 then the equation of directrix is
Any point on the parabola whose focus is (0, 1) and the directrix is x + 2 = 0 is given by -
The locus of the point of intersection of the tangents to the parabola x2 – 4x – 8y + 28 = 0 which are at right angle is -
The ends of a line segments are P (1, 3) and Q (1, 1). R is a point on the line segment PQ such that PR : QR = 1 : λ. If R is an interior point of the parabola y2 = 4x then -
Two unequal parabolas have the same common axis which is the x-axis and have the same vertex which is the origin with their concavities in opposite direction. If a variable line parallel to the common axis meet the parabolas in P and P' the locus of the middle point of PP' is
The equation of the common tangent touching the circle (x – 3)2 + y2 = 9 and the parabola y2 = 4x above the x-axis is -
The tangent at the point P(x1, y1) to the parabola y2 = 4ax meets the parabola y2 = 4a(x + b) at Q and R, the coordinates of the mid-point of QR are
If θ be the angle subtended at the focus by the normal chord at the point (λ, λ),λ ≠ 0 on the parabola y2 = 4ax, then equation of the line through (1, 2) and making and angle θ with xaxis is
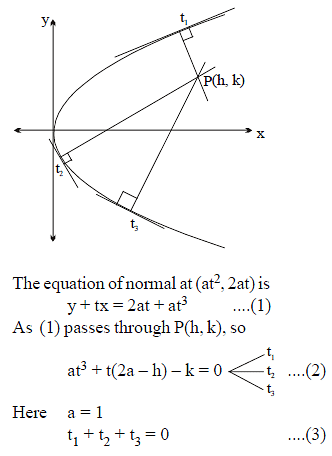
Normals are concurrent drawn at points A, B, and C on the parabola y2 = 4x at P(h, k). The locus of the point P if the slope of the line joining the feet of two of them is 2, is
The length of a focal chord of the parabola y2 = 4ax at a distance b from the vertex is c. Then
Maximum number of common chords of a parabola and a circle can be equal to