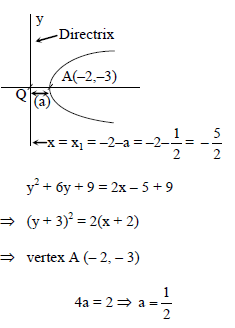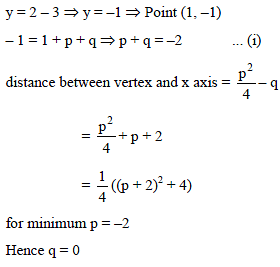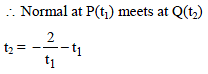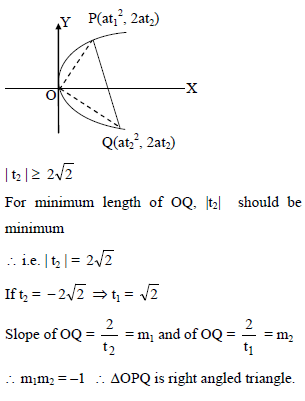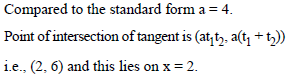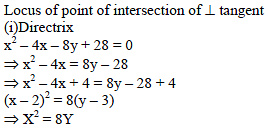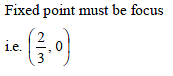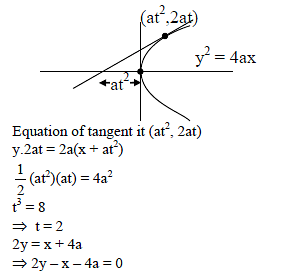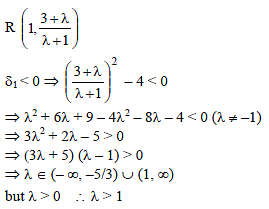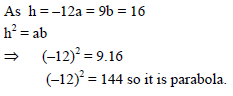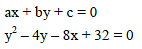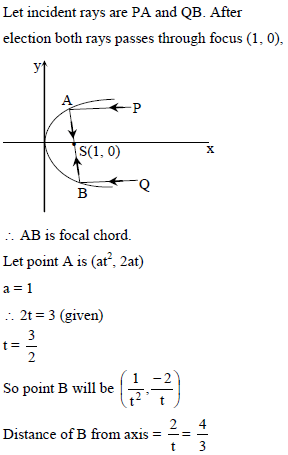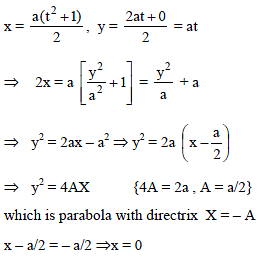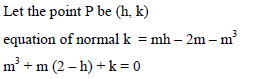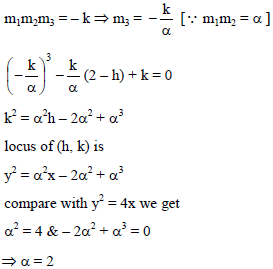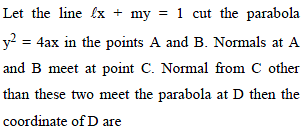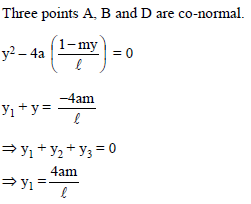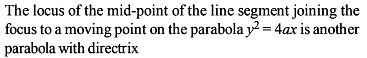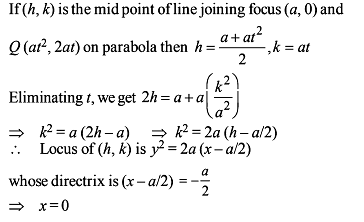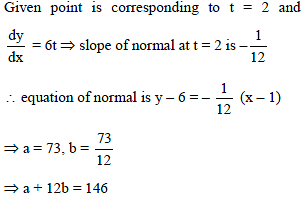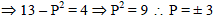Parabola - 2 - JEE MCQ
30 Questions MCQ Test - Parabola - 2
For the parabola y2 + 6y – 2x + 5 = 0
(i) the vertex is (– 2, – 3)
(ii) The directrix is y + 3 = 0
Which of the following is correct ?
The parabola y = x2 + px + q cuts the straight line y = 2x – 3 at a point with abscissa 1 then the values of p and q for which the distance between the vertex of the parabola and the x- axis is the minimum, is -
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If x + 2y + 3 = 0 is a tangent to the parabola y2 = kx then value of k is
If normal at point P on parabola y2 = 4ax, (a > 0) meet it again at Q is such a way that OQ is of minimum length where O is vertex of parabola, then ΔOPQ is
If the tangent at the point P(x1, y1) to the parabola y2 = 4ax meets the parabola y2 = 4a(x + b) at Q and R, then the mid-point of QR is -
Tangents are drawn from a point P to the parabola y2 = 8x such that the slope of one tangent is twice the slope of other. The locus of P is
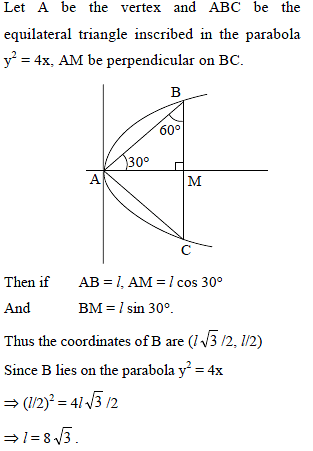
An equilateral triangle is inscribed in the parabola y2 = 4x one of whose vertex is at the vertex of the parabola, the length of each side of the triangle is -
The parametric equation of a parabola is x = 4t2, y = 8t. The tangents at the points whose parameters are 1/2 and 1 meet on the line -
If a ≠ 0 and the line 2bx + 3cy + 4d = 0 passes through the points of intersection of the parabolas y2 = 4ax and x2 = 4ay, then -
The locus of the point of intersection of the tangents to the parabola x2 – 4x – 8y + 28 = 0 which are at right angles is
Chord of contact of two perpendicular tangents of parabola 3y2 = 8x always passes a fixed point which is :
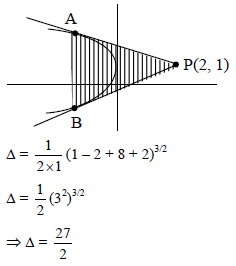
If tangent drawn from point P(2, 1) to the parabola y2 – 2y + 4x + 2 = 0 meet at A & B then area of ΔPAB is ?
The line y = 2x + c is a tangent to the parabola y2 = 16 x, if c equals
If P (at12, 2at1) and Q (at22, 2at2) are two variable points on the curve y2 = 4ax and PQ subtends a right angle at the vertex, then t1t2 is equal to -
The equation of the tangent to the parabola y = (x – 3)2 parallel to the chord joining the points (3, 0) and (4, 1) is-
A tangent to the parabola y2 = 4ax encloses an area of 4a2 with the coordinate axes, the equation of the tangent is
R is a point inside the parabola y2 = 4x and it divide the line segment PQ internally in λ : 1. If P is (1, 3) and Q is (1, 1), then the range of λ is
The general equation of 2nd degree 9x2 –24xy + 16y2 – 20x –15y – 60 = 0 represents
If the line ax +by + c = 0 is a tangent to the parabola y2 – 4y – 8x + 32 = 0, then –
A parabolic mirror is kept along y2 = 4x and two light rays parallel to its axis, are reflected along one straight line. If one of the incident light rays is at 3 units distance from the axis, then the distance of other incident ray from axis will be
The normal chord of a parabola y2 = 4ax at the point whose ordinate is equal to the abscissa, then angle subtended by normal chord at the focus is :
The locus of the mid point of the line segment joining the focus to a moving point on the parabola y2 = 4ax is another parabola with directrix
Normals are drawn from the point P on a parabola y2 = 4x with slopes m1. m2 = α is a part of the parabola it self, then the value of α is
If the normal to the curve x = t – 1, y = 3t2 – 6 at the point (1, 6) make intercepts a and b on x and y-axis respectively, then the value of a + 12b is
Let P(x1, y1) and Q(x2, y2) be points on the curve y = x2 – 5x + 6 at which the tangents drawn intersect at the pont R(1, 1). Find area of triangle PQR.
The value of P such that the vertex of y = x2 + 2px + 13 is 4 unit above the x axis is -