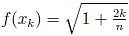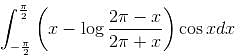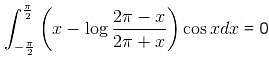GATE Mathematics Mock Test - 2 - Mathematics MCQ
30 Questions MCQ Test - GATE Mathematics Mock Test - 2
The question given below consists of a pair of related words followed by four pain of words. Select the pair that best expresses the relation in the original pair.
LEGEND : MAP ::
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider the differential equestion 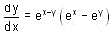 and y = 0 and x → ∞ then
and y = 0 and x → ∞ then 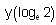 is
is
Convert Cartesian coordinates (2, 6, 9) to Cylindrical and Spherical Coordinates.
Let 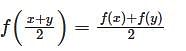 for all real x and y. If f’(0) exists and equals – 1 and f(0) = 1, then find f(2).
for all real x and y. If f’(0) exists and equals – 1 and f(0) = 1, then find f(2).
What is the number of subgroups of S4 of order 12 ?
If 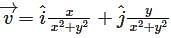 what is the value of this integral
what is the value of this integral 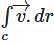 the circular path x2 + y2 = 1 ?
the circular path x2 + y2 = 1 ?
Let there be a vector X = yz2 ax + zx2 ay + xy2 az. Find X at P(3,6,9) in cylindrical coordinates.
In conics, the _____ is revolving to form two anti-parallel cones joined at the apex.
Given f (x) = ex cosy, what is the value of the fifth term in Taylor's series near (1, π/4) where it is expanded in increasing order of degree & by following algebraic identity rule?
In a Binomial Distribution, if p, q and n are probability of success, failure and number of trials respectively then variance is given by
Find the distance between two points A(5,60.,0) and B(10,90.,0) where the points are given in Cylindrical coordinates.
For a third degree monic polynomial, it is seen that the sum of roots are zero. What is the relation between the minimum angle to be rotated to have a Rolles point (α in Radians) and the cyclic sum of the roots taken two at a time c
If x3y2 is an integrating factor of (6y2 + axy)dx + (6xy + bx2)dy =0, a, b ∈ ℝ then
If f(x) = x3 + 3x2 + Sin(x) and g(x) = ex – 1 than find value of 
What is the formula used to find the area surrounded by the curves in the following diagram?
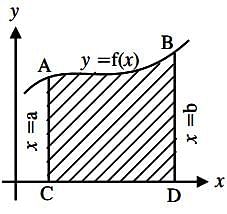
A Function f(x) has the property f(a) = f(b) for ∀a,b…∈….I and a + b = 20 then which of the following even degree polynomials could be f(x)
If f(x) = x2 – 3x + 2 and g(x) = x3 – x2 + x – 1 than find value of 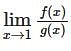
The graph of f(x) passes through the point (-1; 4). The slope of the line tangent to the graph at the point (x; f(x)) is -2x -3. Find f(0).
Find the limit of Riemann sums that is equal to the defnite integral 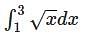
The extremium value of the function z = xy over the plane x + y = 1 is (upto two decimal places) _________.


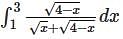
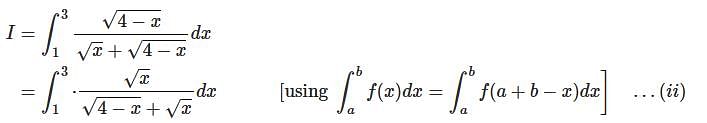
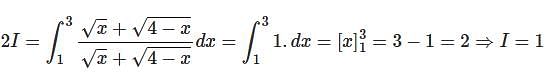
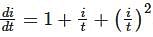 .
.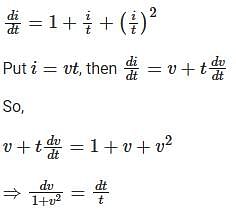
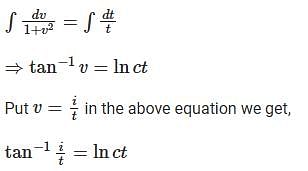

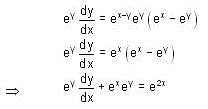
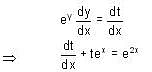
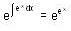
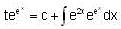
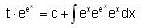
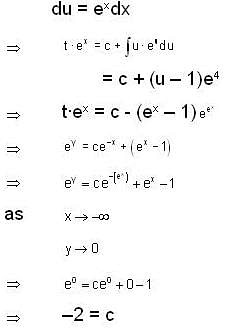
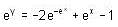
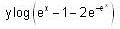
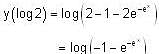
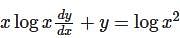 .
.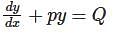

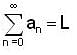 and if
and if 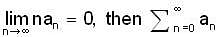 is
is
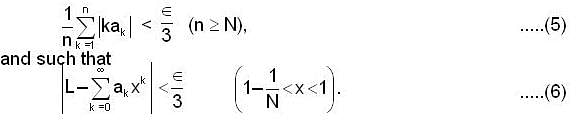
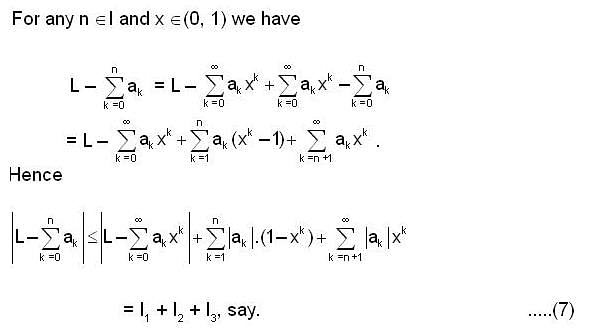
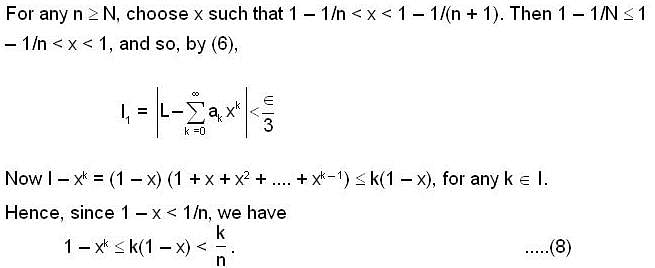
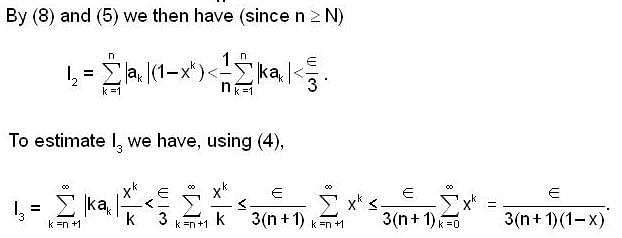
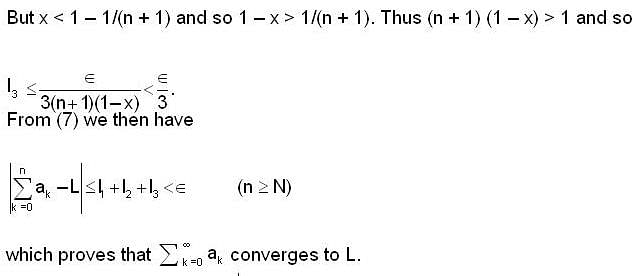
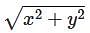 and
and 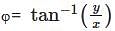 and z = z where (x, y, z) is the Cartesian coordinates. The Spherical coordinates is of the form (r, θ, φ) where
and z = z where (x, y, z) is the Cartesian coordinates. The Spherical coordinates is of the form (r, θ, φ) where 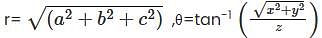 and
and  .Now, substituting the values for x as 2, y as 6 and z as 9, we get the answer as (6.32, 71.565., 9) and (11, 35.097., 71.565.).
.Now, substituting the values for x as 2, y as 6 and z as 9, we get the answer as (6.32, 71.565., 9) and (11, 35.097., 71.565.).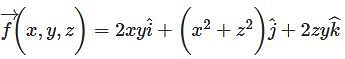 is
is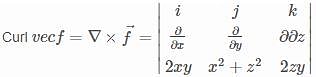
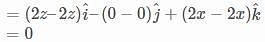
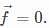
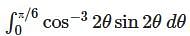 .
.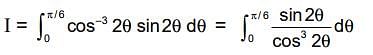
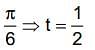
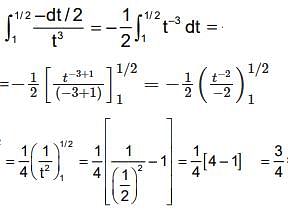
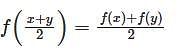
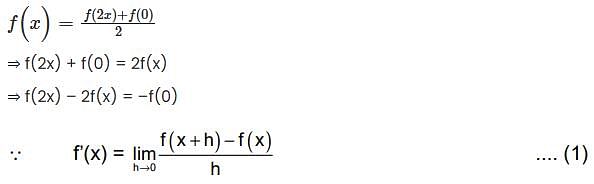


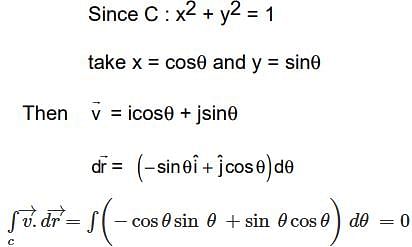
 .
.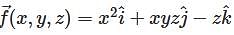 at the point (2,1,-2).
at the point (2,1,-2).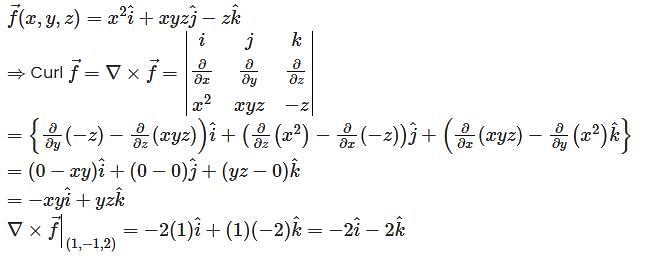
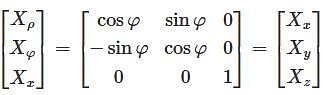
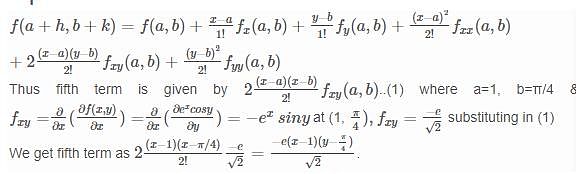
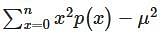
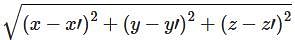 and substituting the values of x, y, and z in it, we get the required answer as 6.19 units. This sum can also be solved using a direct formula to find distance using two points in Cylindrical coordinates.
and substituting the values of x, y, and z in it, we get the required answer as 6.19 units. This sum can also be solved using a direct formula to find distance using two points in Cylindrical coordinates.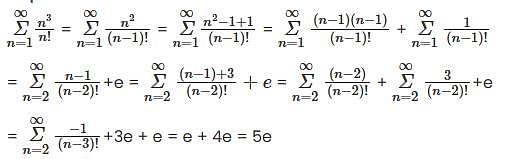
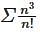 converges and sum is 5e.
converges and sum is 5e.

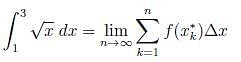
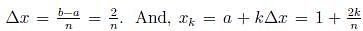 . Iff we let
. Iff we let 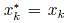 we have
we have