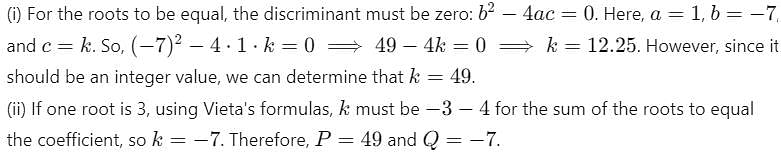HOTs for Maths Olympiad - 3 - Class 10 MCQ
10 Questions MCQ Test - HOTs for Maths Olympiad - 3
Read the given statements and select the incorrect option.
Read the given statements and select the incorrect option.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Read the following statements carefully and state ‘T’ for true and ‘F’ for false.
(i) The sum of the interior angles of a triangle is 180 degrees.
(ii) The area of a triangle with base b and height h is given by 1/2bh.
(iii) The perimeter of an equilateral triangle with side length s is 3s
(ii) The area of a triangle with base b and height h is given by 1/2bh.
(iii) The perimeter of an equilateral triangle with side length s is 3s
Read the following statements carefully and state ‘T’ for true and ‘F’ for false.
(i) The circumference of a circle with radius r is 2πr.
(ii) The area of a circle with diameter d is πd2.
(iii) The volume of a sphere with radius r is 4/3 πr3.
Fill in the blanks and select the correct option.
(i) If the roots of the quadratic equation x2 - 7x + k = 0 are equal, then the value of k is P.
(ii) If one of the roots of the quadratic equation x2 + kx + 12 = 0 is 3, then the value of k is Q.
Fill in the blanks and select the correct option.
(i) The sum of the roots of the quadratic equation ax2 + bx + c = 0 is -b/a. For the equation 2x2 - 4x + 2 = 0, the sum of the roots is P.
(ii) The product of the roots of the same equation is Q.
Read the following statements and select the correct option.
Statement-I: The sum of the roots of the quadratic equation ax2 + bx + c = 0 is -b/a
Statement-II: The product of the roots of the quadratic equation ax2 + bx + c = 0 is c/a
Read the following statements and select the correct option.
Statement-I: The value of logb,(mn) is logb, m + logb, n.
Statement-Il: The value of logb (m/n) is logb m - logb, n.
Solve the following and select the correct option.
(i) If the sum of the squares of two consecutive positive integers is 365, find the integers.
(ii) If the length of the diagonal of a square is 8√2 cm, find the side length of the square.
Solve the following and select the correct option.
(i) Find the sum of the first 20 terms of the arithmetic sequence where the first term is 7 and the common difference is 3.
(ii) If a solid sphere is melted and recast into 8 smaller spheres of equal size, each having a radius 1/2 of the original, find the ratio of the surface area of one of the smaller spheres to that of the original sphere.
Top Courses for Class 10
Important Questions for HOTs for Maths Olympiad - 3
HOTs for Maths Olympiad - 3 MCQs with Answers
Online Tests for HOTs for Maths Olympiad - 3
|
© EduRev
|
Education Revolution
|
|
