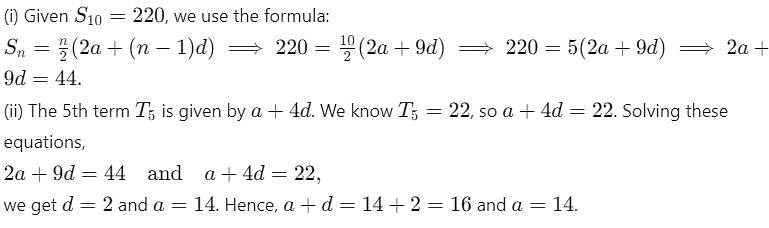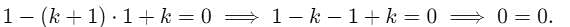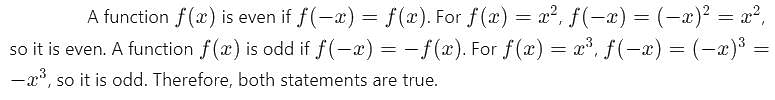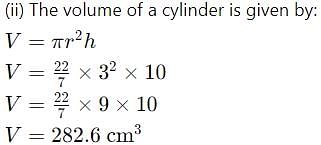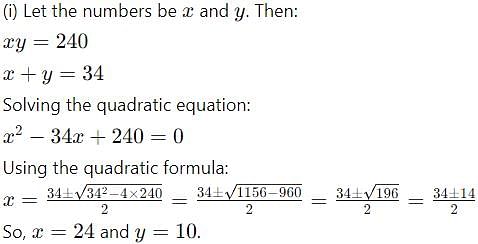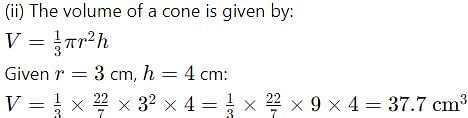All Courses
Get the App Signup / Login
Sign in Open App
Class 10 Exam  >  Class 10 Tests  >  HOTs for Maths Olympiad - 4 - Class 10 MCQ

HOTs for Maths Olympiad - 4 - Class 10 MCQ


Test Description

10 Questions MCQ Test - HOTs for Maths Olympiad - 4

HOTs for Maths Olympiad - 4 for Class 10 2024 is part of Class 10 preparation. The HOTs for Maths Olympiad - 4 questions and answers have been prepared according to the Class 10 exam syllabus.The HOTs for Maths Olympiad - 4 MCQs are made for Class 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for HOTs for Maths Olympiad - 4 below.
Solutions of HOTs for Maths Olympiad - 4 questions in English are available as part of our course for Class 10 & HOTs for Maths Olympiad - 4 solutions in Hindi for Class 10 course. Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free. Attempt HOTs for Maths Olympiad - 4 | 10 questions in 15 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study for Class 10 Exam | Download free PDF with solutions
HOTs for Maths Olympiad - 4 - Question 1
Save

Read the given statements and select the incorrect option.

Detailed Solution for HOTs for Maths Olympiad - 4 - Question 1

The measure of each exterior angle of a regular pentagon is 360°/5 = 72°. Hence, the given statement is correct. The incorrect option here should be revised as "The measure of each exterior angle of a regular pentagon is 60°."

HOTs for Maths Olympiad - 4 - Question 2
Save

Which of the following is not a property of an isosceles triangle?

Detailed Solution for HOTs for Maths Olympiad - 4 - Question 2

An isosceles triangle does not necessarily have all angles equal; it only has two equal angles. Hence, Option C is incorrect.

1 Crore+ students have signed up on EduRev. Have you? Download the App
HOTs for Maths Olympiad - 4 - Question 3
Save

Read the following statements carefully and state ‘T’ for true and ‘F’ for false.
(i) The roots of the quadratic equation x2 − 5x + 6 = 0 are 2 and 3.
(ii) The quadratic equation x2 + 4x + 5 = 0 has real and distinct roots.
(iii) The sum of the roots of the quadratic equation ax2 + bx + c = 0 is given by - b/a

Detailed Solution for HOTs for Maths Olympiad - 4 - Question 3

(i) The quadratic equation x2 - 5x +6 = 0 factors to (x -2)(x -3) = 0, so the roots are 2 and 3. True.
(ii) The quadratic equation x2 + 4x + 5 = 0 has a discriminant of 42 - 4 • 1 • 5 =16 - 20 = -4, which is less than zero, so it has no real roots. False.
(iii) The sum of the roots of the quadratic equation ax2 + bx + c = 0 is given by -b/a. True.

HOTs for Maths Olympiad - 4 - Question 4
Save

Read the following statements carefully and state ‘T’ for true and ‘F’ for false.

(i) The length of the diagonal of a square with side length s is s√2 ​.
(ii) The volume of a cube with side length a is a3.
(iii) The surface area of a cube with side length a is 6a2.
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 4

HOTs for Maths Olympiad - 4 - Question 5
Save

Fill in the blanks and select the correct option.

(i) The sum of the first n terms of an arithmetic progression (AP) is given by Sn = n/2 (2a + (n - 1) d). If the sum of the first 10 terms is 220, then the value of a + d is P.
(ii) If the 5th term of the same AP is 22, then the value of a is Q.
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 5

HOTs for Maths Olympiad - 4 - Question 6
Save

Fill in the blanks and select the correct option.

(i) If the equation x2 - (k + 1)x + k = 0 has one root equal to 1, then the value of k is P.

(ii) The other root of the equation is Q.
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 6

(i) Substituting x = 1 in the equation, we get:

Therefore, k can be any value, but since the other options do not satisfy, k = 0.

(ii) With k = 0, the equation becomes x2 - x = 0, with roots 0 and 1. Thus, the other root is 2.

HOTs for Maths Olympiad - 4 - Question 7
Save

Read the following statements and select the correct option.

Statement-I: The derivative of sin(x) is cos(x).
Statement-Il: The derivative of cos(x) is sin(x).
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 7

The derivative of sin(x) is indeed cos(x), but the derivative of cos(x) is - sin(x), not sin(x). Therefore, Statement-I is true, but Statement-Il is false.

HOTs for Maths Olympiad - 4 - Question 8
Save

Read the following statements and select the correct option.

Statement-I: The function f(x) = x2 is an even function.
Statement-II: The function f (x) = x3 is an odd function.
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 8

HOTs for Maths Olympiad - 4 - Question 9
Save

Solve the following and select the correct option.

(i) A rectangle has a length twice its width. If its perimeter is 36 cm, find the dimensions of the rectangle.
(ii) A cylinder has a height of 10 cm and a radius of 3 cm. Find its volume. Use π 22/7
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 9


HOTs for Maths Olympiad - 4 - Question 10
Save

Solve the following and select the correct option.

(i) The product of two numbers is 240 and their sum is 34. Find the numbers.

(ii) A cone has a base radius of 3 cm and a height of 4 cm. Find its volume. Use π = 22/7
Detailed Solution for HOTs for Maths Olympiad - 4 - Question 10


Information about HOTs for Maths Olympiad - 4 Page
In this test you can find the Exam questions for HOTs for Maths Olympiad - 4 solved & explained in the simplest way possible. Besides giving Questions and answers for HOTs for Maths Olympiad - 4, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 10

Download as PDF

Top Courses for Class 10

Important Questions for HOTs for Maths Olympiad - 4

Find all the important questions for HOTs for Maths Olympiad - 4 at EduRev.Get fully prepared for HOTs for Maths Olympiad - 4 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the HOTs for Maths Olympiad - 4 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of HOTs for Maths Olympiad - 4 resources.

HOTs for Maths Olympiad - 4 MCQs with Answers

Prepare for the HOTs for Maths Olympiad - 4 within the Class 10 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for HOTs for Maths Olympiad - 4

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace HOTs for Maths Olympiad - 4 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup