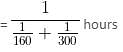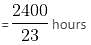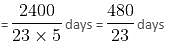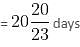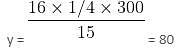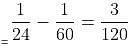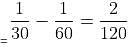Test Level 3: Simple & Compound Interest (September 1) - CAT MCQ
30 Questions MCQ Test - Test Level 3: Simple & Compound Interest (September 1)
Mr. Khanna pays 10% pa interest on an amount borrowed and lends this amount at 12% pa. If at the end of the year, he earns Rs. 2.4 crore as simple interest in the transaction, then what is the sum transacted?
Amit invested two equal sums of Rs. 5000 for 2 years at 10%, one at compound interest payable yearly and the other at compound interest payable half-yearly. Find the difference between amounts that he will get at the end of 2 years.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A certain sum of money lent at simple interest amounts to Rs. 1,300 in 4 years and Rs. 1,525 in 7 years. Find the sum.
A man borrows a certain sum at 20% compounded annually and lends it at 25% simple interest. What is the maximum number of years for which he can wait, so that he does not bear any loss?
Vivek purchased a bike costing Rs. 51,250 under finance with a down payment (which has to be paid at the beginning) of Rs. 9,575. Next month onwards, he has to pay Rs. 1,300 every month up to 36 months to clear the remaining payment. What is the rate of interest under simple interest?
Raghav has to repay a loan of Rs. 12,820 in three annual instalments. The first instalment is to be half of the second and one-third of the third. If the compound interest is calculated annually at a rate of 10%, then find the value of the third instalment that Raghav has to pay.
For a loan of Rs. 32,400 that I gave to my friend Anil, he promised to pay me the amount in monthly installments, starting with a certain amount and increasing the installments every month with a fixed amount of Rs. 100. In this way, he could clear off the loan in 24 months. How much was the first installment?
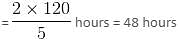
A sum of Rs. 9400 is divided into three parts, such that the simple interests accrued on these sums for three, four and five years are equal. Find the amount deposited for five years.
If a person repaid Rs. 22,500 after 10 years of borrowing a loan, at 10% per annum simple interest find out what amount did he take as a loan?
Mr. X , a very industrious person, wants to establish his own unit. For this he needs an instant loan of Rs. 5,00,000 and, every five years he requires an additional loan of Rs.100,000. If he had to clear all his outstandings in 20 years, and he repays the principal of the first loan equally over the 20 years, find what amount he would have to pay as interest on his initial borrowing if the rate of interest is 10% p.a. Simple Interest.
A and B work together for 8 days to complete a piece of work and B and C work together for 12 days to complete the same work. C alone can complete the work in 24 days and A is twice as efficient as B. How much time does it take to complete the work if all the three work together?
A, B and C can do a piece of work in 20, 30 and 40 days, respectively. A and C started the work and B joined 4 days later. A left 8 days before the completion of work and C was also absent for 5 days in between. How many days will it take for the work to be completed?
A group of employees is working on a project. If 10 more employees join them, then the project will be completed in 2/3 of the time. If the work has to be completed in 1/3 of the time, then how many more employees have to join?
A can do a piece of work in 20 days, working 8 hours a day and B can do the same work in 30 days, working 10 hours a day. If both A and B work together for 5 hours a day, how many days will they take to complete the same work?
A and B together can complete a piece of work in 25 days. B and C together can complete the same work in 30 days. How many days would A and C take to complete the work?
The amount of work done by a man on nth day after starting a piece of work is n times the amount of work that can be done on the first day. If 8 men start the work, it can be completed in 10 days. How many men should work if the work has to be completed in 4 days?
A man started a piece of work on the first day. The second day, one more person joined him. The next day, one more person joined. Everyday, one new person joined until the work got completed. If the work was completed in 15 days, how many days would 10 men take to complete the same work, given that they worked regularly and efficiency of all men is the same?
If 300 men could do a piece of work in 16 days, then how many men would do 1/4 of the same work in 15 days?
A alone can finish a piece of work in 12 days and B alone can do it in 18 days. If they work together and finish it, then out of total wages of Rs. 50, A will get
Two inlet pipes A and B can fill a tank in 24 hours and 30 hours, respectively. An outlet pipe C can empty the tank in 60 hours. The pipe C is continuously open and the pipes A and B work on alternate hours, starting with A. How much time does it take to fill the tank?
Directions: Read the information carefully and answer the question.
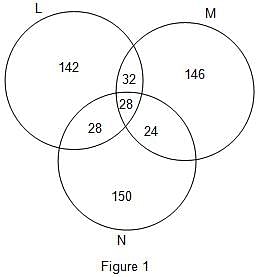
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. How many candidates were selected by company L?
Directions: Read the information carefully and answer the question.
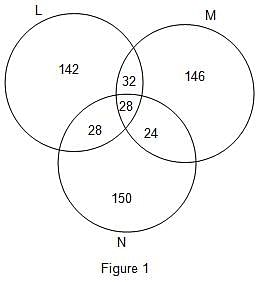
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. Find the total number of candidates who were selected only by company L or M.
Directions: Read the information carefully and answer the question.
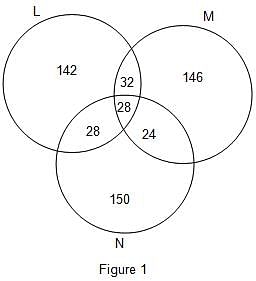
Three companies L, M and N participated for campus recruitment in college Z. All the three companies selected an equal number of candidates. There were 60 candidates who were selected by L and M both. The number of candidates selected by both M and N was 68 less than twice the number of candidates selected by both L and M. There were 28 candidates who got placed in all the 3 companies. This number was 50% less than the number of candidates selected by both L and N. The total number of candidates selected by both L and N was 91.88% less than total number of candidates selected by all the three company.
Q. What is the total number of candidates who were placed in exactly two companies only?
Directions: Study the given information and answer the following question.
A talent hunt competition was being conducted by a TV Channel. As they were expecting variations in the type of talent, they appointed 7 different judges: Karan Johar, Geeta Basra, Himesh Reshamia, Anu Malik, Mika, Farah Khan and Pritam. In the first round, 6 contestants namely Rahul, Reema, Ram, Rita, Raju and Riya appeared before the panel for selection. Accidentally, the organisers forgot to mention the marks for which they were to be evaluated; therefore, each of the judges evaluated the contestants on a different total marks. The total marks for which the judges evaluated all the contestant were 100, 150, 50, 125, 150, 50 and 75 in the exact order of judges as mentioned above, respectively. The table mentioned below presents the percentage score of the contestants by each of the judges.
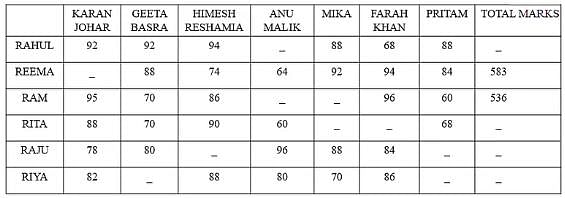
Q. What is the ratio of the total marks obtained by Rita from Karan Johar, Geeta Basra and Anu Malik to the total marks obtained by Rahul from Pritam, Mika and Farah Khan?
Directions: Study the given information and answer the following question.
A talent hunt competition was being conducted by a TV Channel. As they were expecting variations in the type of talent, they appointed 7 different judges: Karan Johar, Geeta Basra, Himesh Reshamia, Anu Malik, Mika, Farah Khan and Pritam. In the first round, 6 contestants namely Rahul, Reema, Ram, Rita, Raju and Riya appeared before the panel for selection. Accidentally, the organisers forgot to mention the marks for which they were to be evaluated; therefore, each of the judges evaluated the contestants on a different total marks. The total marks for which the judges evaluated all the contestant were 100, 150, 50, 125, 150, 50 and 75 in the exact order of judges as mentioned above, respectively. The table mentioned below presents the percentage score of the contestants by each of the judges.

Q. If the total marks given by Geeta and Pritam to Riya are one mark less than marks granted to Rahul by Geeta and Himesh, then what is the overall percentage of marks obtained by Riya?
Directions: Study the given information carefully to answer the question that follows:
In a college, there are 2400 students studying in different branches - Electronics, Mechanical, Electrical, IT, and Computer Science. The ratio of the number of boys to that of girls is 5 : 3. 12% boys study in the Electronics branch. 24% girls study in the Mechanical branch. The ratio of the number of boys to that of girls in the Electronics branch is 6 : 11. One-ninth of girls study in the Computer Science branch. 42% boys study in the IT branch. The number of girls studying in the IT branch is 10% of the boys studying in the same branch. The remaining girls study in the Electrical branch. The total number of students studying in the Computer Science branch is 285. 22% boys study in the Electrical branch. The remaining boys study in the Mechanical branch.
Q. What percentage of the total girls in the college do the girls in the IT branch constitute?
Directions: Study the given information carefully to answer the question that follows:
In a college, there are 2400 students studying in different branches - Electronics, Mechanical, Electrical, IT, and Computer Science. The ratio of the number of boys to that of girls is 5 : 3. 12% boys study in the Electronics branch. 24% girls study in the Mechanical branch. The ratio of the number of boys to that of girls in the Electronics branch is 6 : 11. One-ninth of girls study in the Computer Science branch. 42% boys study in the IT branch. The number of girls studying in the IT branch is 10% of the boys studying in the same branch. The remaining girls study in the Electrical branch. The total number of students studying in the Computer Science branch is 285. 22% boys study in the Electrical branch. The remaining boys study in the Mechanical branch.
Q. The number of boys studying in the Mechanical branch is approximately what percentage of the total number of boys in the college?
Directions: Read the following information and answer the question that follows.
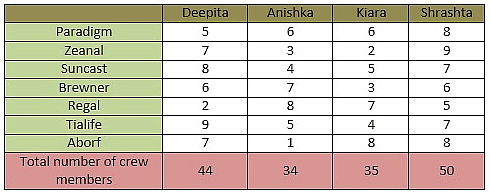
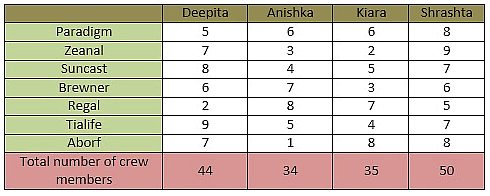
Four actresses - Deepita, Anishka, Kiara and Shrashta have dedicated some of their crew members to look after their public relations image in some top news agencies - Paradigm, Zeanal, Suncast, Brewner, Regal, Tialife and Aborf.
- Not more than 9 crew members are dedicated to one agency by any actress.
- Deepita and Shrashta have dedicated the greatest number of crew members an actress can send to Tialife and Zeanal, respectively.
- Anishka, Kiara and Shrashta have dedicated 4, 5 and 2 members less than the number of crew members dedicated by Deepita to Tialife.
- Sum of crew members of Deepita dedicated to Tialife and to Suncast is 17.
- Number of crew members of Anishka dedicated to Regal, Kiara dedicated to Aborf and Shrashta dedicated to Paradigm as well as to Aborf is the same as the number of crew members of Deepita dedicated to Suncast.
- Number of crew members of Shrashta dedicated to Tialife and to Suncast is the same and the number of crew members of Shrashta dedicated to Suncast and to brewner are consecutive numbers.
- Number of crew members of Deepita, Anishka, Kiara and Shrashta dedicated to Brewner, Paradigm, Paradigm and Brewner, respectively is the same.
- Sum of crew members of Shrashta dedicated to Brewner and to Regal is 11.
- Shrashta has the greatest number of crew members dedicated to news agencies, while Deepita has 6 less and Kiara has 15 less.
- Number of crew members dedicated by Shrashta to Regal is the same as the number of crew members of Kiara dedicated to Suncast and of Deepita dedicated to Paradigm.
- Deepita has 7 members each, dedicated both to Zeanal and to Aborf.
- Anishka has 10 crew members less than Deepita.
- Crew members of Deepita dedicated to Aborf are the same as the crew members of Anishka dedicated to Brewner.
- Anishka has 3 and 4 members dedicated to Zeanal and to Suncast, respectively. Kiara has 2 and 7 members dedicated to Zeanal and to Regal, respectively.
- Number of crew members of Deepita dedicated to Regal is not the same as the number of crew numbers of Anishka dedicated to Aborf.
Q. What is the sum of crew members of all actresses that are dedicated to Suncast and to Tialife?
Directions: Read the following information and answer the question that follows.
Four actresses - Deepita, Anishka, Kiara and Shrashta have dedicated some of their crew members to look after their public relations image in some top news agencies - Paradigm, Zeanal, Suncast, Brewner, Regal, Tialife and Aborf.
- Not more than 9 crew members are dedicated to one agency by any actress.
- Deepita and Shrashta have dedicated the greatest number of crew members an actress can send to Tialife and Zeanal, respectively.
- Anishka, Kiara and Shrashta have dedicated 4, 5 and 2 members less than the number of crew members dedicated by Deepita to Tialife.
- Sum of crew members of Deepita dedicated to Tialife and to Suncast is 17.
- Number of crew members of Anishka dedicated to Regal, Kiara dedicated to Aborf and Shrashta dedicated to Paradigm as well as to Aborf is the same as the number of crew members of Deepita dedicated to Suncast.
- Number of crew members of Shrashta dedicated to Tialife and to Suncast is the same and the number of crew members of Shrashta dedicated to Suncast and to brewner are consecutive numbers.
- Number of crew members of Deepita, Anishka, Kiara and Shrashta dedicated to Brewner, Paradigm, Paradigm and Brewner, respectively is the same.
- Sum of crew members of Shrashta dedicated to Brewner and to Regal is 11.
- Shrashta has the greatest number of crew members dedicated to news agencies, while Deepita has 6 less and Kiara has 15 less.
- Number of crew members dedicated by Shrashta to Regal is the same as the number of crew members of Kiara dedicated to Suncast and of Deepita dedicated to Paradigm.
- Deepita has 7 members each, dedicated both to Zeanal and to Aborf.
- Anishka has 10 crew members less than Deepita.
- Crew members of Deepita dedicated to Aborf are the same as the crew members of Anishka dedicated to Brewner.
- Anishka has 3 and 4 members dedicated to Zeanal and to Suncast, respectively. Kiara has 2 and 7 members dedicated to Zeanal and to Regal, respectively.
- Number of crew members of Deepita dedicated to Regal is not the same as the number of crew numbers of Anishka dedicated to Aborf.
Q. What is the sum of crew members of Deepita, Kiara and Shrashta that are dedicated to Regal?
Directions: Answer the question on the basis of the information given below.
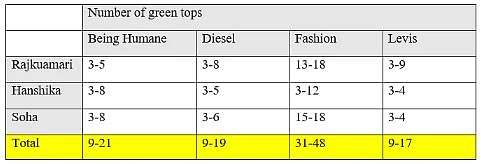
Anisha has a big collection of tops. The top with her is of one or the other of the four brands namely Being Humane, Diesel, Fashion and Levis. The colour of the tops with her is either pink or green. Out of the tops with her, Anisha has bought only a few of them whereas the rest are gifted to her by one or the other of her six friends namely Ankita, Rajkumari, Usha, Hanshika, Sunita and Soha. Anisha does not know the exact number of tops gifted to her but she knows that the number of green tops of each brand gifted to her by each of her mentioned friends is at least 3 and at most 18. Further, the number of pink tops of each brand gifted to her by each of his mentioned friends is at least 7 and at most 25.
Anisha asked her boyfriend to help her determine the number of tops gifted to her by each of her mentioned friends. In turn, her boyfriend provided her with the information listed in the table given below:
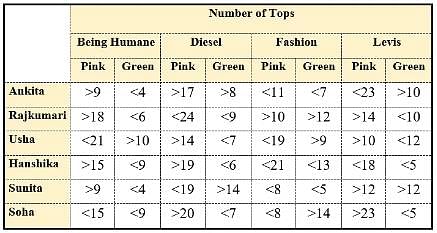
Q. Out of the green tops gifted to Anisha by Rajkumari, Hanshika and Soha, the number of green tops of brand 'Being Humane' is definitely less than the number of green tops of brand:


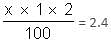
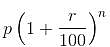
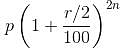
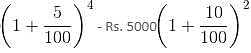
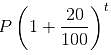
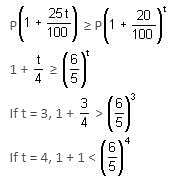
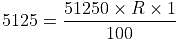
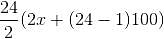 = Rs. 32,400
= Rs. 32,400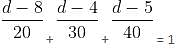
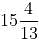 days
days