Mathematical Statistics - 2017 Past Year Paper - IIT JAM MCQ
30 Questions MCQ Test - Mathematical Statistics - 2017 Past Year Paper
The imaginary parts of the eigenvalues of the matrix
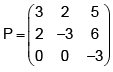
are
Let 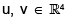 be such that u = (1 2 3 5)T and v = (5 3 2 1)T. Then the equation uvT x = v has
be such that u = (1 2 3 5)T and v = (5 3 2 1)T. Then the equation uvT x = v has

Which of the following statements is TRUE ?
be a sequence defined as follows :
Which of the following statements is TRUE ?
Let X be a continuous random variable with the probability density function
Let X be a random variable with the moment generating function
Then P(X > 1) equals
Let X be a discrete random variable with the probability mass function
p(x) = k(1 + |x|)2, x = –2, –1, 0, 1, 2,
where k is a real constant. Then P(X = 0) equals
Let the random variable X have uniform distribution on the interval . Then P(cos X > sin X) is
be a sequence of i.i.d. random variables having common probability density function
Let X1, X2, X3 be a random sample from a distribution with the probability density function
Which of the following estimators of θ has the smallest variance for all θ > 0 ?
Player P1 tosses 4 fair coins and player P2 tosses a fair die independently of P1. The probability that the number of heads observed is more than the number on the upper face of the die, equals
Let X1 and X2 be i.i.d. continuous random variables with the probability density function
Using Chebyshev’s inequality, the lower bound of
Let X1, X2, X3 be i.i.d. discrete random variables with the probability mass function
Let Y = X1 + X2 + X3. Then P(Y > 5) equals
Let X and Y be continuous random variables with the joint probability density function
where c is a positive real constant. Then E(X) equals
Let X and Y be continuous random variables with the joint probability density function
Let X1, X2, ..., Xm, Y1, Y2, ..., Yn be i.i.d. N(0, 1) random variables. Then
has
be a sequence of i.i.d. random variables with the probability mass function
then possible values of m and M are
Let x1 = 1.1, x2 = 0.5, x3 = 1.4, x4 = 1.2 be the observed values of a random sample of size four from a distribution with the probability density function
Then the maximum likelihood estimate of θ2 is
be the observed values of a random sample of size four from a distribution with the probability density function
Then the method of moments estimate of θ is
Let X1, X2 be a random sample from an N(0, θ) distribution, where θ > 0. Then the value of k, for which the interval is a 95% confidence interval for θ, equals
Let X1, X2, X3, X4 be a random sample from N(θ1, σ2) distribution and Y1, Y2, Y3, Y4 be a random sample from N(θ1, σ2) distribution, where θ1, θ2 ∈ (-∞, ∞) and σ > 0. Further suppose that the two random samples are independent. For testing the null hypothesis H0 : θ1 = θ2 against the alternative hypothesis H1 : θ1 > θ2, suppose that a test rejects H0 if and only if
The power of the tes
Let X be a random variable having a probability density function f ∈ {f0, f1}, where
For testing the null hypothesis against
based on a single observation on X, the power of the most powerful test of size α = 0.05 equals
Consider the function
f(x, y) = x3 – y3 – 3x2 + 3y2 + 7, x,
Then the local minimum (m) and the local maximum (M) of f are given by
let the sequence
be defined by
Then the values of c for which the seriesconverges are
If for a suitable α > 0,
exists and is equal to
Let
Which of the following statements is TRUE ?
Let Q, A, B be matrices of order n × n with real entries such that Q is orthogonal and A is invertible. Then the eigenvalues of QT A–1 BQ are always the same as those of
be the curve defined by
Let L be the length of the arc of this curve from the origin to the point P on the curve at which the tangent is perpendicular to the x- axis. Then L equals














