Mathematical Statistics - 2016 Past Year Paper - IIT JAM MCQ
30 Questions MCQ Test - Mathematical Statistics - 2016 Past Year Paper
Let α , β,γ be real numbers such that β ≠ 0 and γ ≠ 0. Suppose
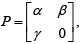
and P-1 =P. Then
Let m > 1. The volume of the solid generated by revolving the region between the y-axis and the curve xy = 4, 1 < y < m, about the y-axis is 15π. The value of m is
Consider the region S enclosed by the surface z = y2 and the planes z = 1,x = 0, x = 1, y = -1 and y = 1. The volume of S is
Let X be a discrete random variable with the moment generating function
Then P (X < 1) equals
Let E and F be two independent events with
Then P(E) equals
Let X be a continuous random variable with the probability density function
Then E (X2)
The probability density function of a random variable X is given by
Then the distribution of the random variable Y = loge X-2a is
Let X1 ,X2 ,..... be a sequence of i.i.d. N (0,1) random variables. converges in probability to
Consider the simple linear regression model with n random observations Yi = β0+ β1xi + εi, i = 1,....,n, (n > 2). β0 and β1 are unknown parameters, x1,....,xn are observed values of the regressor variable and ε1... ,εn are error random variables with E (εi) = 0, i = 1,....,n, and for i, j = 1,...., n, For real constants
is an
unbiased estimator of β1 , then
Let (X, Y) have the joint probability density function
Then P(Y <1 | X = 3) equals
Let X1,X2,..... be a sequence of i.i.d. random variables having the probability density function
If the distribution of
converges to N ( 0,1) as
n → ∞, then a possible value of α is
Let X1,...,Xn be a random sample from a population with the probability density function
If Tn = min {X1,...,Xn}, then
Let X1,...,Xn be i.i.d. random variables with the probability density function
If X(n) = max {X1,...,Xn},
Let X and Y be two independent N ( 0,1) random variables. Then P (0 < X2 + Y2 < 4) equals
Let X be a random variable with the cumulative distribution function
Then E (X) equals
Let X1,....,Xn be a random sample from a population with the probability density function
For a suitable constant K, the critical region of the most powerful test for testing H0 : θ =1 against H1 : θ = 2 is of the form
Let X1,...,Xn, Xn+1, Xn+2,..., Xn+m (n > 4,m > 4) be a random sample from N (μ ,σ2);
then the distribution of the random variable
is
Let X1,...,Xn (n > 1) be a random sample from a Poisson (θ) population, θ > 0, and Then the uniformly minimum variance unbiased estimator of θ2 is
Let X be a random variable whose probability mass functions f(x | H0) (under the null hypothesis H0) and f (x |H1) (under the alternative hypothesis H1) are given by
For testing the null hypothesis H0 : X~f (x | H0) against the alternative hypothesis H1 : X~f (x | H1), consider the test given by: Reject
If α = size of the test and β = power of the test, then
Let X1,..,Xn be a random sample from a N (2θ, θ2) population, θ > 0. A consistent estimator for θ is
An institute purchases laptops from either vendor V1 or vendor V2 with equal probability. The lifetimes (in years) of laptops from vendor V1 have a U (0, 4) distribution, and the lifetimes (in years) of laptops from vendor V2 have an Exp (12) distribution. If a randomly selected laptop in the institute has lifetime more than two years, then the probability that it was supplied by vendor V2 is
Let y (x) be the solution to the differential equation
Let an = e -2n sin n and bn = e-n n2 (sin n)2 for n >1. Then
be a twice differentiable function. Further, let f (0) = 1, f(2) = 2 and f(4) = 3. Then
Let f (x,y) = x2 - 400 x y2 for all (x,y) Then f attains its
Let y (x) be the solution to the differential equation
Then y (1) equals
The area between the curve y = g" (x) and the x-axis over the interval [0, 2] is
singular matrix such that
for a nonzero vector
and
Then



















