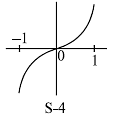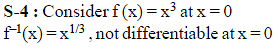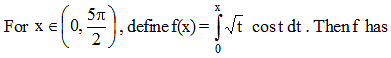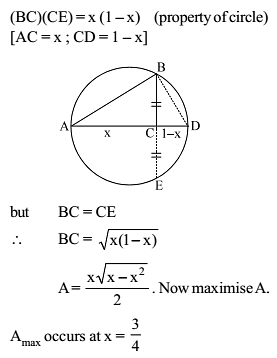Test: Maxima and Minima of a Function(15 Sep) - JEE MCQ
10 Questions MCQ Test - Test: Maxima and Minima of a Function(15 Sep)
The maximum and minimum values of f(x) = 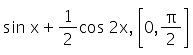 are
are
The maximum value of f (x) = sin x in the interval [π,2π] is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24 x – 18x2
If f (x) = a log |x| + bx2 + x has extreme values at x = –1 and at x = 2, then values of a and b are
Find the maximum and minimum values of f (x) = 2x3 – 24x + 107 in the interval [1, 3].
Give the correct order of initials T or F for following statements. Use T if statement is true and F if it is false.
Statement-1: If f : R → R and c ∈ R is such that f is increasing in (c – δ, c) and f is decreasing in (c, c + δ) then f has a local maximum at c. Where δ is a sufficiently small positive quantity.
Statement-2 : Let f : (a, b) → R, c ∈ (a, b). Then f can not have both a local maximum and a point of inflection at x = c.
Statement-3 : The function f (x) = x2 | x | is twice differentiable at x = 0.
Statement-4 : Let f : [c – 1, c + 1] → [a, b] be bijective map such that f is differentiable at c then f–1 is also differentiable at f (c).
A right triangle is drawn in a semicircle of radius 1/2 with one of its legs along the diameter. The maximum area of the triangle is